Anthony R. West - Solid State Chemistry and its Applications

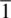The left‐hand diagram gives the equivalent positions in space group . These are represented by large open circles; a positive sign indicates that they are above the plane of the paper and a negative sign below. In the latter case, that position will lie in the unit cell below the one that has been defined. A comma inside the equivalent position symbol indicates an enantiomorphic relationship to a second, centrosymmetrically related equivalent position.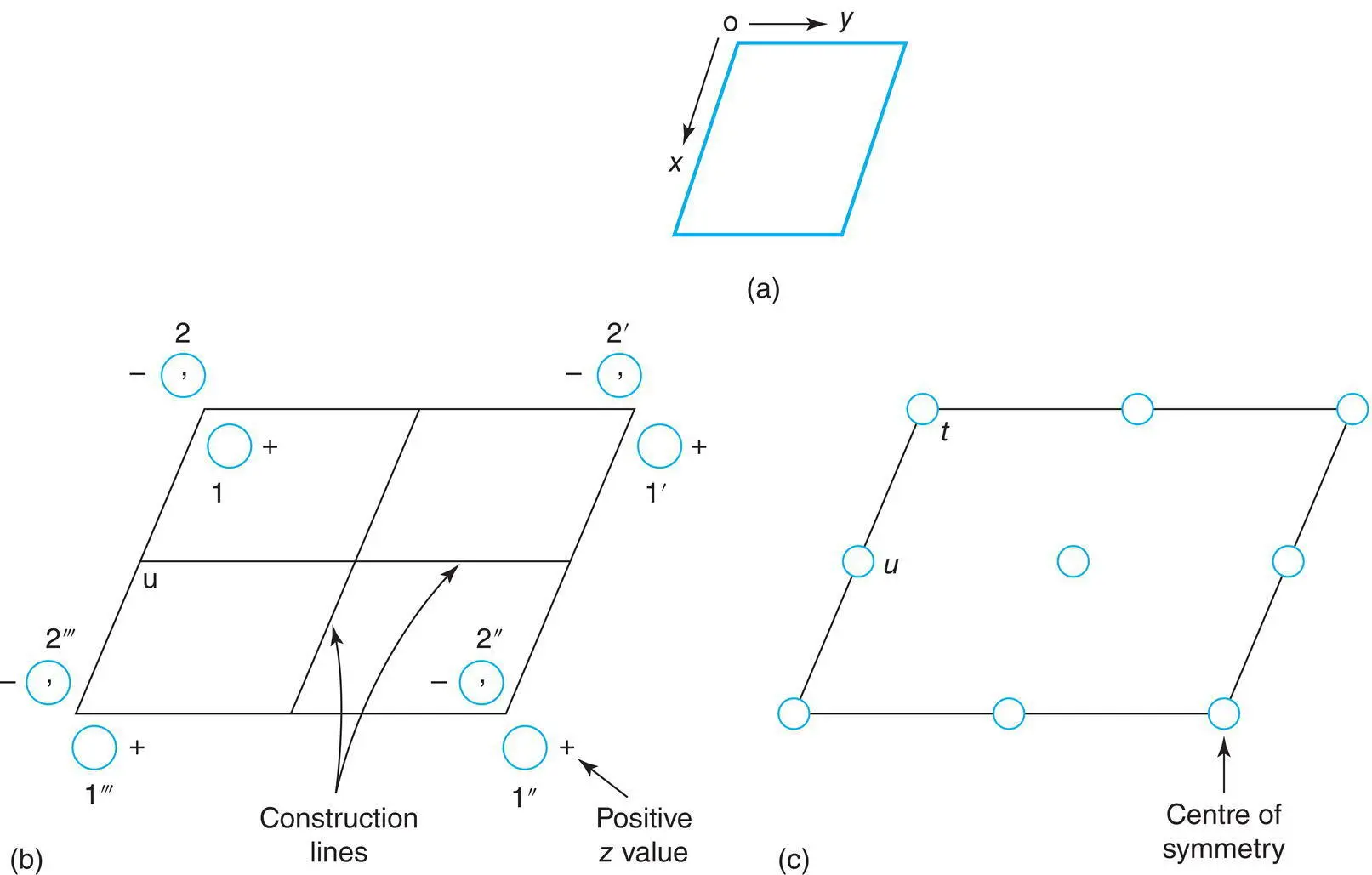

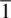To find the equivalent positions in the space group, it is necessary, as with point groups, to choose a starting position and operate on this position with the various symmetry elements that are present. The conventional starting position is at 1, close to the origin and with small positive values of x, y and z . This position must be present in all other unit cells (definition of the unit cell); three are shown as 1′, 1″ and 1‴.

Figure 1.60 (a) The convention used to label axes and origin of space groups. (b, c) Triclinic space group P (number 2); coordinates of equivalent positions: x, y, z; .

Consider now the effect of the centre of symmetry, t , at the origin of the unit cell. This acts upon position 1 to create position 2. The minus sign at 2 indicates a negative z height and the comma shows its enantiomorphic relation to position 1. Positions 2′, 2″ and 2‴ in Fig. 1.60 are automatically generated from position 2 by translation because they are equivalent positions in adjacent cells.

To understand the meaning of an enantiomorphic relationship, the effect of an inversion operation is to convert a left‐handed object into a right‐handed one and vice versa. This is illustrated in Fig. 1.61 for two tetrahedra that are positioned so as to be related to each other by inversion through a centre of symmetry. Individual tetrahedra do not possess a centre of symmetry, whereas groupings of tetrahedra may possess one, such as shown in Fig. 1.61. In addition, if the tetrahedra themselves are chiral, such as the molecule CHFBrI with the four different corners represented by 1, 2, 3, 4 in Fig. 1.61, then the centrosymmetric partner in the configuration shown is a different isomer with the corner arrangement 1′, 2′, 3′, 4′.

The next step is to write down the coordinates of the equivalent positions in the unit cell. This is done in the form x, y, z where x , y and z are the fractional distances, relative to the unit cell edge dimensions, from the origin of the cell. Let position 1, Fig. 1.60, have fractional coordinates x, y, z ; positions 1′, 1″ and 1‴ in adjacent unit cells are given by adding 1 to the relevant coordinates i.e. x , 1 + y , z for 1′, 1 + x, 1 + y, z for 1″ and 1 + x, y, z for 1‴. Position 2 is the centrosymmetric partner position of 1, i.e. − x , − y, − z . Position 2″ is then in the next unit cell at⋯1 – x , 1 – y, –z , etc. Thus, if a position lies outside the unit cell under consideration, an equivalent position within the unit cell can be found, usually by adding or subtracting 1 from one or more of the fractional coordinates. Position 2 ″ is outside the cell because it has a negative z value; the equivalent position inside the cell is given by a displacement of one unit cell length in the z direction to give coordinates 1 – x , l – y , 1 – z . These coordinates are written in shorthand as , , .

Figure 1.61 Two tetrahedra in a centrosymmetric arrangement.

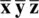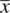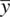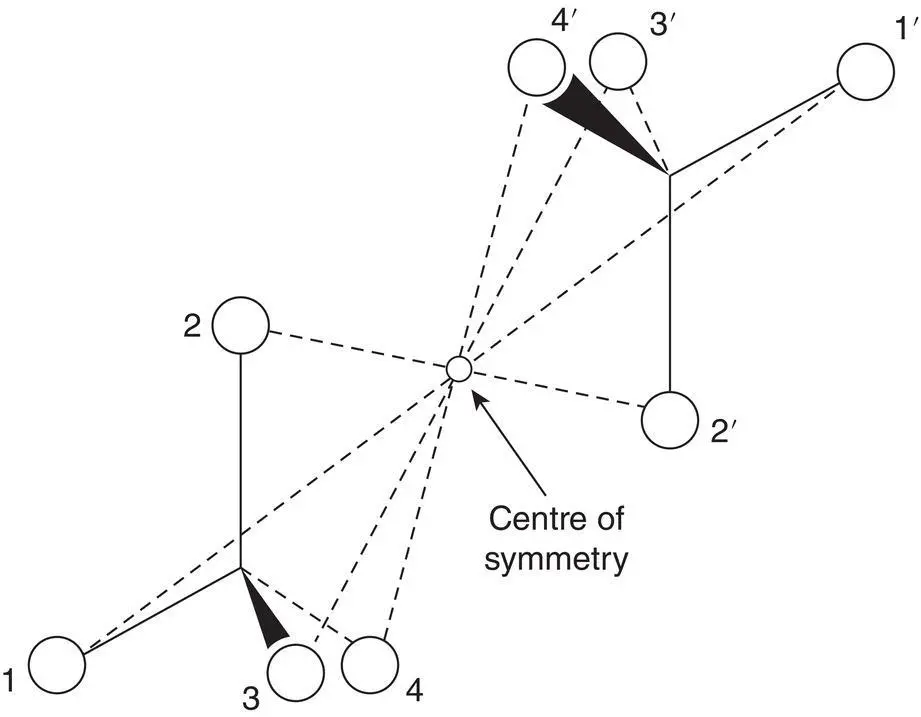
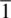In summary, therefore, the unit cell in space group P has two equivalent positions that lie inside the unit cell: x , y, z (position 1) and 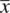, , 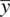(the position at height с above 2″ in Fig. 1.60).

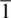Although only one centre of symmetry is necessary to generate the equivalent positions in P , many other centres of symmetry are created automatically. For example, the centre of symmetry at и arises because pairs of positions such as 1 and 2‴, 2 and 1‴, etc., are centrosymmetrically related through u . This may be seen from the diagram or may be proven by comparing coordinates of the three positions: positions 2‴ and 1 are equidistant from и and lie on a straight line that passes through u .

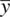The positions x , y, z and , , are general positions and apply to any value of x , у, z between 0 and 1. In certain circumstances, x , y, z and 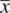, ½, coincide, for example, if x = y = z = ½. In this case, there is only one position, ½,½,½ which is a special position. Special positions arise when the general position lies on a symmetry element, in this case a centre of symmetry, as discussed for point groups in Section 1.18.3. The coordinates of the one‐fold special positions in P 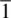are, therefore, (0, 0, 0), (½, 0, 0), (0, ½, 0), (0, 0, ½), (½, ½, 0), (½, 0, ½), (0, ½, ½) and (½, ½, ½), and correspond to the corner, edge, face and body centres of the unit cell.