In most other hexagonal perovskites, the metal‐metal pair interactions do not extend as far as forming infinite columns of face‐sharing octahedra in a complete hcp anion array, as in BaNiO 3. Thus, pairs of face‐sharing octahedra occur in BaRuO 3which are linked by corner‐sharing to adjacent pairs to give the ch sequence, as shown in (i); this may be written more completely as ( ch ) 2to indicate that two pairs form the repeat in the c unit cell direction and is alternately given the label 4H, referring to a 4‐layer repeat unit with overall hexagonal symmetry. In hexagonal BaTiO 3, face‐sharing pairs are separated by single layers of a cubic structure, (j), to give the polytype ( cch ) 2. In Ba 8Ta 4Ti 3O 12, (k), the stacking sequence is ( cchc ) 2and in Ba 10Ta 7.04Ti 1.2O 30(l), the sequence is ( cchcc ) 2. Many materials with more complex polytypic sequences have also been synthesised; overviews of these and other perovskite‐derivative structures, including those containing two types of cp layers which introduce an additional structural complexity, are given in the books by Tilley and Mitchell.
A recent development that has given fresh impetus to the study of hexagonal perovskite derivative phases is the discovery of a high level of oxide ion conductivity in Ba 3MNbO 8.5:M = Mo, W. The structure is a hybrid of two separate structures: first, a 9‐layer hexagonal perovskite, ( hhc ) 3of formula A 3B 2O 9that contains face‐sharing trimers of octahedra linked through their corners; second, a structurally related, but oxygen‐deficient palmierite structure in which (i) one of the AO 3layers has instead the stoichiometry AO 2, (ii) the B cations are displaced from their octahedral sites to form layers of tetrahedra and (iii) the overall formula is A 3B 2O 8. Given the wide range of hexagonal perovskites and their derivatives that are already known, many of which are similarly oxygen‐deficient, the discovery of other new oxide ion conducting materials in this family, as well as possible mixed conductors, may be anticipated.
1.17.8 Rhenium trioxide (ReO 3), perovskite tungsten bronzes, tetragonal tungsten bronzes and tunnel structures
The structure of cubic ReO 3is closely related to the perovskite described above. It is the same as the ‘TiO 3’ framework of perovskite, SrTiO 3, but without the Sr atoms. Its unit cell is the same as that shown in Fig. 1.41(a) with Re at corners and O at edge centres. A few oxides and halides form the ReO 3structure, Table 1.20, together with an example of the anti‐ReO 3structure in Cu 3N.
A wide variety of oxide and oxyfluoride structures, often with complex formulae, can be derived from the ReO 3structure by coupled rotation of groups of octahedra. To see this, we start with the ideal cubic ReO 3structure shown in Fig. 1.43(a). Each octahedron shares its six corners with other octahedra and in 2D, layers of corner‐sharing octahedra are obtained. In the cubic perovskite structure, large 12‐coordinate cavities are occupied by A cations, ideally without modification of the array of octahedra, (b).
The perovskite tungsten bronze structures are intermediate between ReO 3and perovskite. They occur in series such as Na xWO 3and have a 3D framework of WO 6octahedra, as in ReO 3, but with some (0 < x < 1) of the large A sites occupied by Na. To accommodate a variation in stoichiometry, x , the oxidation state of tungsten is a mixture of, or intermediate between, V and VI. The formula of the bronzes may be written more completely as

These materials have interesting colours and electrical properties. At low x , they are pale green/yellow in colour and semiconducting. As x rises and electrons begin to occupy the 5 d band of tungsten, they become brightly coloured and metallic, hence the name ‘bronze’.
Table 1.20 Some compounds with the ReO3 structure
| Compound |
a /Å |
Compound |
a /Å |
| ReO 3 |
3.734 |
NbF 3 |
3.903 |
| UO 3 |
4.156 |
TaF 3 |
3.9012 |
| MoF 3 |
3.8985 |
Cu 3N |
3.807 |
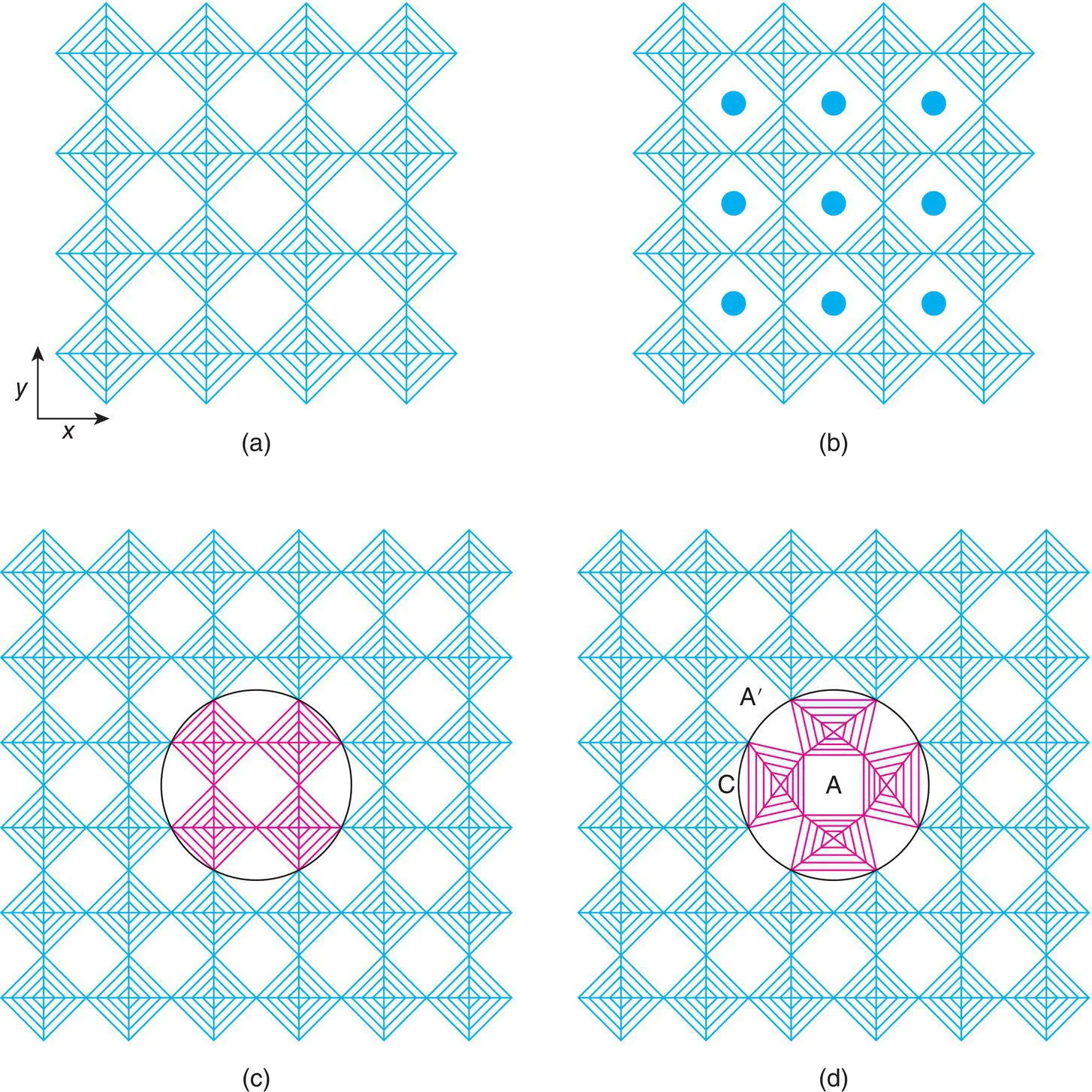
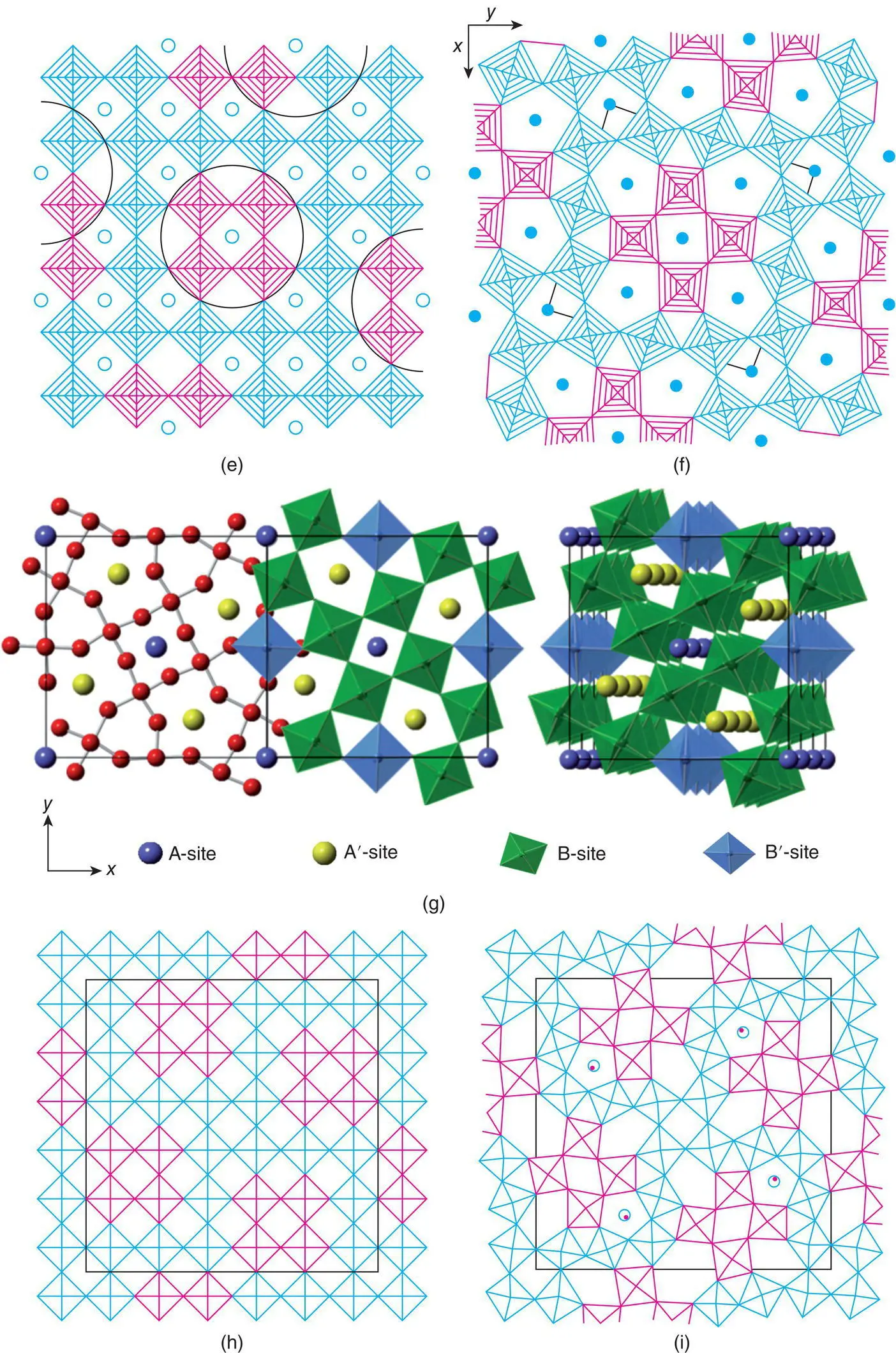
Figure 1.43 The structure of (a) ReO3, (b) tungsten bronze NaxWO3, (c, d) bronze and tunnel structures derived from ReO3 by rotation of blocks of four octahedra and (e, f) the tetragonal tungsten bronze structure.
Adapted from B. G. Hyde and M. O'Keeffe, Acta Cryst. Sect. A29, 243 (1973).
(g) The TTB structure of Ba2LaTi2Nb3O15.
Adapted from G. C. Miles et al., J. Mater. Chem. 15, 798 (2005).
(h, i) Tunnel structure of Mo5O14.
A variety of monovalent cations enter the tungsten bronze structure; similar series also occur with MoO 3in the molybdenum bronzes . Many other highly conducting bronzes based on oxides MO 2or MO 3form in which M is a transition metal, such as Ti, V, Nb, Ta, Mo, W, Re, Ru or Pt, that is capable of existing in mixed oxidation states.
Thus far, we have not modified the arrangement of octahedra. Different arrays of octahedra are, however, obtained by rotation of columns of four octahedra by 90° and reconnecting them with the parent structure as shown in Fig. 1.43(c) and (d). This has major consequences for the size and coordination number of the A cation sites. Some, A, retain their coordination number of 12 and in projection may be perceived as ‘square tunnels’; a second set of sites, A′, has a coordination number which is increased to 15 and in projection may be regarded as “pentagonal tunnels’. A third set, C, has coordination number reduced to nine and is referred to as ‘triangular tunnels’. We now have the building blocks for the tetragonal tungsten bronze, TTB, structure. This contains an important family of ferroelectric materials although, since they are insulating, it is rather a misnomer to call them bronzes.
Table 1.21 Some compounds with the tetragonal tungsten bronze, TTB, structure. Unit cell: tetragonal a 12.4, c 3.9 Å
| A 2 |
A′ |
B 4B′ |
O 15 |
| Ba 2 |
RE a |
Ti 2, Nb 3 |
O 15 |
| Sr 2 |
Na or K |
Nb 5 |
O 15 |
| Ba 2 |
Na |
Nb 5 |
O 15 |
| Ba 2or Sr 2 |
Ba or Sr |
Ti, Nb 4 |
O 15 |
| Sr 2.5 |
|
Nb 5 |
O 15 |
| K 0.4–0.6 |
|
W |
O 3 |
a RE = La, …, Dy, Bi.
The general formula of the ideal TTB structure is A 2A′B 4B′O 15or A 2A′B 3B′ 2O 15, depending on the oxidation states of A, A′, B, and B′. The structure is built of corner‐sharing BO 6and B′O 6octahedra; the B,B′:O ratio is 1:3, as in ReO 3, but the linkage of the octahedra is different from that in ReO 3. In the TTB structure, blocks of octahedra which form four‐membered rings are rotated by 90° relative to the parent ReO 3structure to give a framework containing triangular, square and pentagonal columns, Fig. 1.43(e) and (f). In the c direction, the unit cell is only one octahedron thick. In principle, all the sites are available for cation occupancy. In practice, large cations such as K +and Ba 2+occupy the pentagonal tunnels with a coordination number to the oxygen of 15, whereas somewhat smaller cations such as La 3+occupy square tunnels with coordination number 12; the triangular tunnels, C in the formula, remain either empty or occupied by smaller ions such as Li +.
Читать дальше















