4 EBE techniques select particular instances of the dataset to explain the behavior of ML models. The approach is mostly model agnostic since they make any ML model more interpretable. The slight difference from model‐agnostic methods is that the EBE methods interpret a model by selecting instances of the dataset and not by acting on features or transforming the model.
Two versions of this technique are (i) Prototypes and Criticisms and (ii) Counterfactual Explanations (CE).
Prototypes a nd criticisms: Prototypes are a selection of representative instances from the data [86–88]; thus, item membership is determined by its similarity to the prototypes, which leads to overgeneralization. To avoid this, exceptions have to be identified also, called criticisms: instances that are not well represented by those prototypes. Kim [89] developed an unsupervised algorithm for automatically finding prototypes and criticisms for a dataset, called Maximum Mean Discrepancy‐critic (MMD‐critic). When applied to unlabeled data, it finds prototypes and critics that characterize the dataset as a whole.
Counterfactual explanations (CE): Wachter et al. [90] presented the concept of “unconditional counterfactual explanations” as a novel type of explanation of automated decisions. CE describe the minimum conditions that would have led to an alternative decision (e.g., a bank loan being or not being approved), without the need to describe the full logic of the algorithm. The focus here is on explaining a single prediction in contrast to adversarial examples, where the emphasis is on reversing the prediction and not explaining it [91]. As the research contributions in this class of methods are actively growing, new model‐agnostic techniques are regularly proposed. In the next section, we will present in more detail some of the techniques listed in this section.
4.2 Relevance Propagation in ANN
Classification of images has become a key ingredient in many computer vision applications, for example, image search, robotics, medical imaging, object detection in radar images, or face detection. A particularly popular approach to the problem is based on the use of neural networks.
This lack of interpretability in these solutions is due to the nonlinearity of the various mappings that process the raw image pixels to its feature representation and from that to the final classifier function. This is a considerable drawback in classification applications, as it prevents human experts from carefully verifying the classification decision. A simple yes or no answer is sometimes of limited value in applications where questions like where something occurs or how it is structured are more relevant than a binary or real‐valued one‐dimensional assessment of mere presence or absence of a certain structure. In this section, we aim to explain in more detail the relation between classification and interpretability for multilayered neural networks discussed in the previous chapter.
4.2.1 Pixel‐wise Decomposition
We start with the concept of pixel‐wise image decomposition, which is designed to understand the contribution of a single pixel of an image x to the prediction f ( x ) made by a classifier f in an image classification task. We would like to find out, separately for each image x , which pixels contribute to what extent to a positive or negative classification result. In addition, we want to express this extent quantitatively by a measure. We assume that the classifier has real‐valued outputs with mapping f : ℝ V→ ℝ 1such that f ( x ) > 0 denotes the presence of the learned structure. We are interested in finding out the contribution of each input pixel x (d)of an input image x to a particular prediction f ( x ). The important constraint specific to classification consists in finding the differential contribution relative to the state of maximal uncertainty with respect to classification, which is then represented by the set of root points f ( x 0) = 0. One possible way is to decompose the prediction f ( x ) as a sum of terms of the separate input dimensions x d:
(4.1) 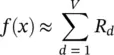
Here, the qualitative interpretation is that R d< 0 contributes evidence against the presence of a structure that is to be classified, whereas R d> 0 contributes evidence for its presence. More generally, positive values should denote positive contributions and negative values, negative contributions.
LRP: Returning to multilayer ANNs, we will introduce LRP as a concept defined by a set of constraints. In its general form, the concept assumes that the classifier can be decomposed into several layers of computation, which is a structure used in Deep NN. The first layer are the inputs, the pixels of the image; and the last layer is the real‐valued prediction output of the classifier f . The l ‐th layer is modeled as a vector 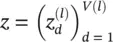 with dimensionality V ( l ). LRP assumes that we have a relevance score
with dimensionality V ( l ). LRP assumes that we have a relevance score  for each dimension
for each dimension 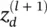 of the vector z at layer l + 1. The idea is to find a relevance score
of the vector z at layer l + 1. The idea is to find a relevance score 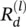 for each dimension
for each dimension 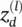 of the vector z at the next layer l which is closer to the input layer such that the following equation holds:
of the vector z at the next layer l which is closer to the input layer such that the following equation holds:
(4.2) 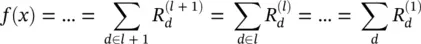
Iterating Eq. (4.2)from the last layer, which is the classifier output f ( x ), back to the input layer x consisting of image pixels then yields the desired Eq. (4.1). The relevance for the input layer will serve as the desired sum decomposition in Eq. (4.1). In the following, we will derive further constraints beyond Eqs. (4.1)and (4.2)and motivate them by examples. A decomposition satisfying Eq. (4.2)per se is neither unique, nor it is guaranteed that it yields a meaningful interpretation of the classifier prediction.
As an example, suppose we have one layer. The inputs are x ∈ ℝ V. We use a linear classifier with some arbitrary and dimension‐specific feature space mapping φ dand a bias b :
(4.3) 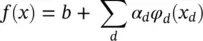
Let us define the relevance for the second layer trivially as 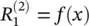 . Then, one possible LRP formula would be to define the relevance R (1)for the inputs x as
. Then, one possible LRP formula would be to define the relevance R (1)for the inputs x as
Читать дальше

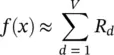
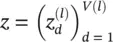 with dimensionality V ( l ). LRP assumes that we have a relevance score
with dimensionality V ( l ). LRP assumes that we have a relevance score  for each dimension
for each dimension 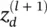 of the vector z at layer l + 1. The idea is to find a relevance score
of the vector z at layer l + 1. The idea is to find a relevance score 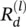 for each dimension
for each dimension 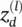 of the vector z at the next layer l which is closer to the input layer such that the following equation holds:
of the vector z at the next layer l which is closer to the input layer such that the following equation holds: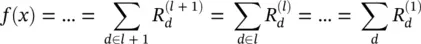
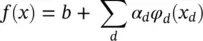
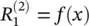 . Then, one possible LRP formula would be to define the relevance R (1)for the inputs x as
. Then, one possible LRP formula would be to define the relevance R (1)for the inputs x as










