where v is the lattice phonon vibration frequency, K is the transition probability constant, k is Boltzmann’s constant, F is the Helmholtz free energy = Et−ΔST, and ΔS is the entropy change associated with the transition. Thus:
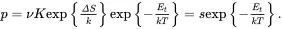 (2.2)
(2.2)
Here, s is known as the “attempt-to-escape” frequency (also known as the “frequency factor,” or the “pre-exponential factor”), with units of s –1. It is the number of times per second that energy is absorbed from phonons in the lattice, and the term exp{−EtkT} is the probability that the energy absorbed is enough to cause a transition from the localized state to the conduction band. Typically, one can expect s ~ 10 12–10 14s –1; that is, of the order of the lattice vibration frequency, v, but differing from it by the factor Kexp{ΔSk}.
By applying equilibrium statistics, it is possible to show that:
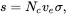 (2.3)
(2.3)
where, Nc is the concentration of available states in the conduction band (units, m –3), ve is the thermal velocity of free electrons (m.s –1) and σ is the capture cross-section for the trap (m 2).
The concentration of free electrons, nc at any given temperature may be written:
 (2.4)
(2.4)
Since the occupancy of the conduction band is essentially zero at the top of the conduction band, the integral can be taken to infinity. It is also assumed that Ec – EF >> kT , which is a good approximation in insulators, even for T = 1000s K. Nc can, therefore, be considered to be the effective density of states of a fictional level lying at the conduction band edge and is defined by:
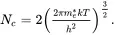 (2.5)
(2.5)
Similarly, the number of free holes in the valence band is given by:
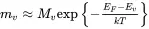 (2.6)
(2.6)
and
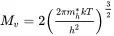 (2.7)
(2.7)
is the density of available states in the valence band. In Equations 2.5and 2.7, me* and mh* are the effective masses of the free electrons and free holes in the conduction and valence bands, respectively, and h is Planck’s constant.
The value of the capture cross-section σ is critically dependent upon the potential distribution in the neighborhood of the trap and, in particular, upon whether the trap is coulombic attractive, neutral, or repulsive. Three representative cases are illustrated in Figure 2.6. The figures show the potential distribution around a coulombic attractive trap (a), a coulombic neutral trap (b), and a coulombic repulsive trap (c). The critical distance rc is that distance for which the energy of coulombic attraction equals the kinetic energy KE of the free electron (Rose 1963). If the trap has a coulombic net charge of +1, then:
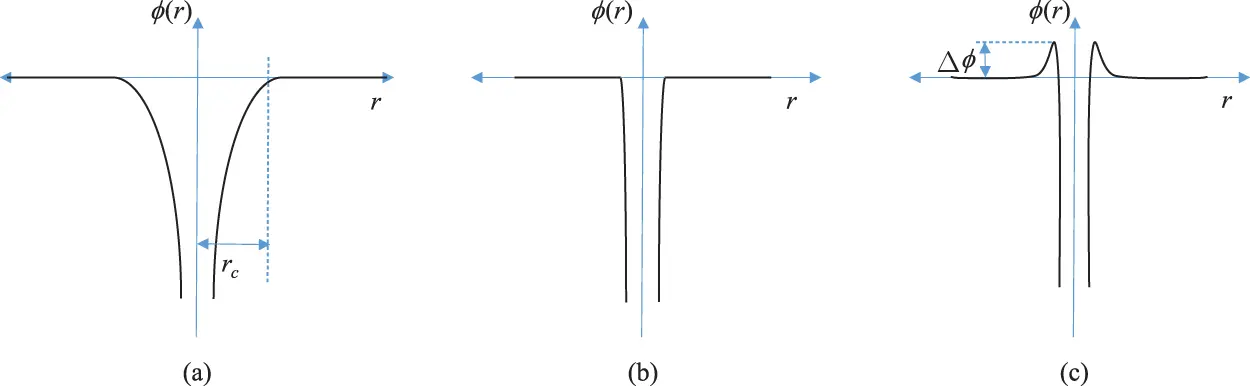
Figure 2.6 Potential ϕ as a function of distance r in the vicinity of: (a) coulombic attractive, (b) neutral, and (c) repulsive localized states. The critical distance rc , where σ=πrc2, is defined in the text. For coulombic repulsive centers the capture cross-section σ is reduced exponentially as a function of the potential barrier Δϕ.
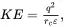 (2.8)
(2.8)
where, q is the charge on the electron and ε is the dielectric constant of the material. From this:
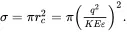 (2.9)
(2.9)
For coulombic repulsive centers the capture cross-section σ is reduced exponentially as a function of the potential barrier Δϕ – i.e. by exp{−qΔϕkT}. Thus, the capture cross-section of a repulsive trap is exponentially dependent on temperature.
Experimentally determined values for σ range from ~10 –16m 2for attractive centers (so-called giant traps) to ~10 –26m 2for repulsive centers. Also, since ve∝T1/2, then KE∝T, and σ∝T−2 for attractive or neutral centers. It is clear that a coulombic attractive trap for a free electron is a repulsive trap for a free hole, and vice-versa. Thus, each localized state is represented by two cross-sections, one for electrons, σe and one for holes, σh. If σe>>σh the state is defined as an electron trap, while for a hole trap σh>>σe.
Apart from thermal excitation out of the localized state, there is also the possibility that the trapped electron might attract an oppositely charged hole and the two may recombine. If a recombination event is more likely that a detrapping event, the localized state is called a recombination center. If the opposite is true, it is a trap. Thus, one can imagine that at a given temperature T , there may exist a state for which the probabilities are equal, that is:
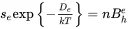 (2.10)
(2.10)
for electrons, and
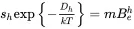 (2.11)
(2.11)
for holes. In these expressions, the left-hand side of the equation represents the probability of thermal excitation from the trap and the right-hand side represents the probability of recombination with the carrier of opposite sign. The definitions of the terms are: se and sh are the attempt-to-escape frequencies for the trapped electrons and the trapped holes, respectively; n and m are the concentrations of trapped electrons and holes; Bhe and Beh are the probabilities of recombination for electrons with holes and vice-versa, expressed in units m 3.s –1. In turn, these are defined as Bhe=σheve and Beh=σehvh, where σhe and σeh are the cross-sections for the capture of electrons by holes, and holes by electrons, respectively and ve and vh are the free electron and free hole thermal velocities. The fictional energies De and Dh are those energies for which Equations 2.10and 2.11are true, and are known as the “Demarcation Levels,” one for electrons and one for holes. They are illustrated in Figure 2.1b. For electron and hole localized levels at energy depths Ete and Eth , such that Ete > De and Eth < Dh , the localized states are traps; for energies EF < Ete < De and EF > Eth > Dh , the localized states are recombination centers. In this way it is clear that recombination centers tend to have energies near the center of the band gap, whereas trap energies are toward the upper (for electrons) or lower (for holes) regions of the gap.
Читать дальше

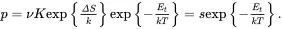 (2.2)
(2.2)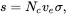 (2.3)
(2.3) (2.4)
(2.4)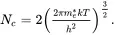 (2.5)
(2.5)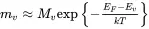 (2.6)
(2.6)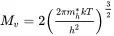 (2.7)
(2.7)
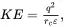 (2.8)
(2.8)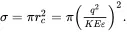 (2.9)
(2.9)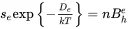 (2.10)
(2.10)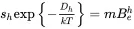 (2.11)
(2.11)