Stephen W. S. McKeever - A Course in Luminescence Measurements and Analyses for Radiation Dosimetry

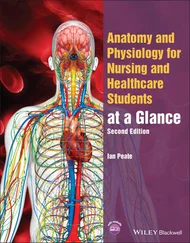
Figure 2.4 (a) Schematic view of a LiF lattice with Mg 2+impurity substituting for a Li +host ion and charge compensated by a Li-vacancy in a <110> direction, forming a dipolar complex; (b) example trimer cluster of three Mg 2+-Li vacdipoles.

An additional consideration, not indicated in the conceptual Figures 2.2 and 2.4, is that the radius of the impurity ions generally do not match those of the host ions for which they substitute. For example, the radius of a Mg 2+ion is 86×10 –12m, whereas the radius of Li +is 90×10 –12m. This small change in radius (<5%) causes a much larger change in ionic volume in that part of the lattice and substituting a Li +ion with a Mg 2+ion results in a decrease of ionic volume by ~15%. Similarly, Ti 4+results in a ~76% volume decrease, while Y 3+in CaF 2causes a ~69% decrease when substituting for Ca 2+. These effects immediately cause lattice distortions over and above distortions due to coulombic forces. 1

Radiation-dosimetry-quality LiF does not contain only Mg impurities; the TL sensitivity of the material is strongly enhanced by the inclusion of Ti 4+impurities. Charge compensation in this case appears through the incorporation of OH –impurities, forming Ti-OH complexes. The role of the Ti-OH complexes in the production of TL is still not precisely determined but they are believed to be active in the recombination processes occurring in this material. In particular, much evidence has accumulated in recent years to suggest that the main TL peak from this material (the so-called peak 5) is the result of a Mg-trimer/Ti-OH complex of an as-yet-undetermined crystalline structure. That is, the Ti-OH complexes and the Mg-Li vactrimers appear to be spatially associated in the LiF lattice and many of the characteristic TL properties of peak 5, and the TL glow curve in general, are uniquely affected by this association.

It is the breakdown in the lattice periodic potential caused by defects that gives rise to energy levels within the forbidden gap. The wavefunctions of electrons in a crystal with perfect periodicity are delocalized and extend throughout the material. States where the electron wavefunction is localized are not allowed. It is when the periodicity breaks down due to the presence of a defect that localized wavefunctions occur. These decay with distance away from the center of the defect over several lattice sites and the corresponding energies reside within the band gap.

Whether they are relatively simple defects or complex defects, interactions between the localized electrons and holes can take place either, or both, non-locally (i.e. via the delocalized bands) or locally (e.g. tunneling of charge between localized states) depending upon both the energy and the spatial association between the defects. The energy levels may be discrete (i.e. characterized by a single energy value) or, because of their complexity, can be distributed in energy with the exact energy value depending upon the nature of the surrounding environment and the presence of other defects. This is especially true of non-crystalline materials such as glasses, in which the surrounding lattice may display short- or long-range disorder, resulting in a range of energies for a particular defect type.

In addition to point defects, one can also add even more complex defects consisting of line dislocations (boundaries between slipped and un-slipped lattice planes), grain boundaries, angular misfits between lattice planes, planar dislocations (internal surfaces), nanoparticle formations, inclusions, and precipitates. Another obvious cause of the breakdown in the periodicity of a lattice is the presence of a surface. Crystals are not infinitely large and at a surface the lattice periodicity ends abruptly giving rise to broken bonds and bonds passivated by the possible presence of foreign atoms, resulting in large concentrations of localized levels at the surface. Clearly, powdered materials with small grain sizes and large surface-to-volume ratios are more likely to exhibit effects due to surface states than larger, bulk materials.

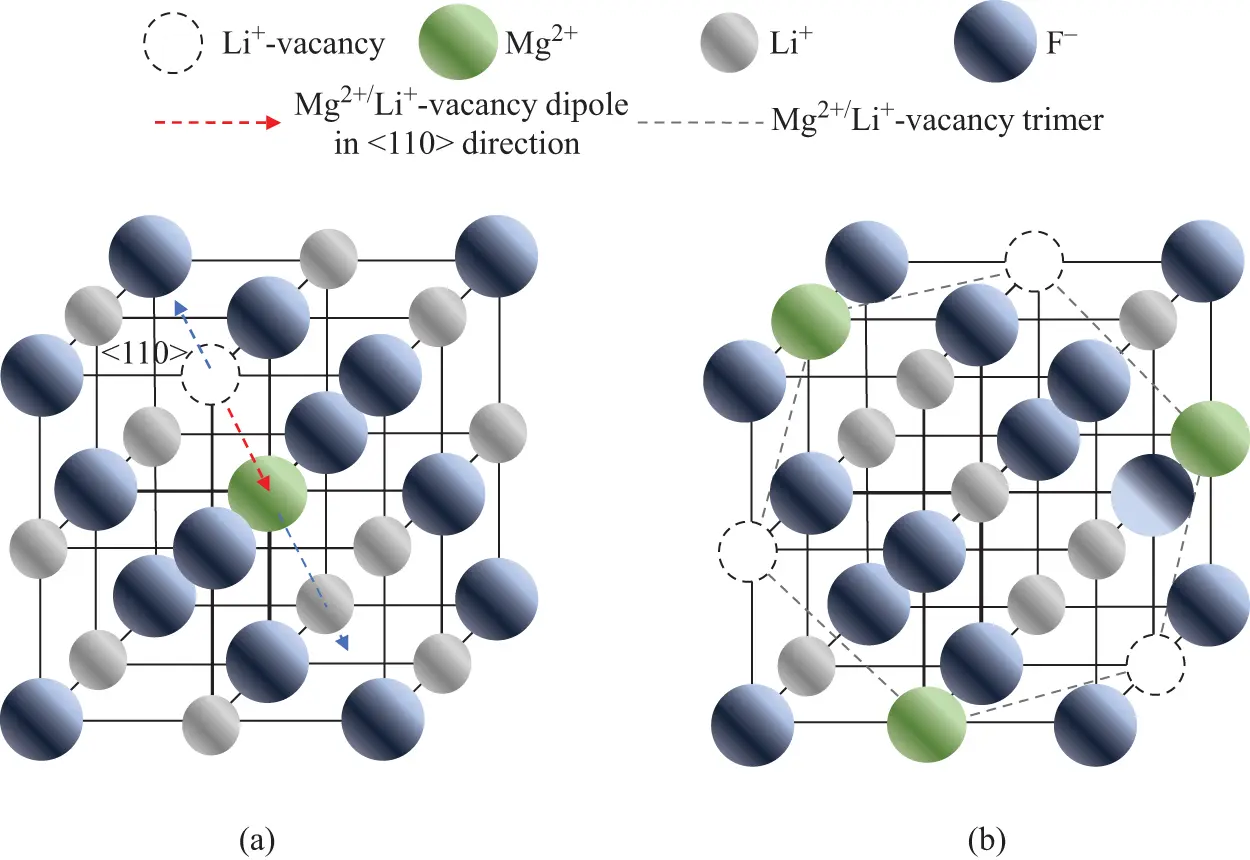
An obvious example of a material in which the infinite periodicity of the lattice cannot be expected is a non-crystalline or glassy material. The amorphous nature of such materials means that, at best, only short-range order can be expected and once several lattice distances are considered the material cannot be defined by regular order. As a result, the presence of defects such as those described in the previous sections results in a range of potential energies to describe the defect, depending upon the local environment. Furthermore, the energy states available to free electrons and holes must be reconsidered in such materials, as shown in Figure 2.5 where the density of allowed states of a crystalline material (Figure 2.5a) is compared with that of an amorphous material (Figure 2.5b). As with crystalline materials, allowed energy zones do exist, but with non-crystalline materials the density of states Z ( E ) partially extends into the gap, creating so-called band-tail states. Defect state energies are distributed rather than discrete and can extend above or below the Fermi Level, EF , such that Z ( EF ) ≠ 0. Localized energy levels (shaded in Figure 2.5b) require absorption of external energy (thermal or optical) to ionize the defects, i.e. to excite the charge carriers (electrons or holes) into the delocalized bands (conduction and valence bands). Thus, a non-crystalline solid can be treated in much the same way as a crystalline solid in the sense that the delocalized bands are separated by an energy gap (more correctly termed a “mobility gap” since Z ( E ) tail states extend into the gap) with localized states due to defects existing within the gap but with distributions of energy (band-tail states).

Figure 2.5 Density of states functions Z ( E ) for (a) a crystalline solid, and (b) an amorphous (non-crystalline) solid. For non-crystalline materials the density of states extends into the band gap (band-tail states) and localized states (shaded) are distributed in energy.

It should also be mentioned that even crystalline materials can exhibit band-tail states extending into the gap if they exhibit sufficient lattice disorder due to variations in bond lengths, bond angles, local density fluctuations, and/or contain high concentrations of impurities or other extrinsic defects. If the disorder is sufficiently high, it can give rise to a density of states Z ( E ) that extends into the band gap. Such materials may include, for example, natural minerals, such as the feldspar family or the various polymorphs of silicon dioxide.

Consider an electron localized at a lattice defect, at energy Et below the conduction band and probability p that the electron will absorb external energy and be excited from the trap into the conduction band. If the temperature of the system is T , the probability per second p that the electron will be thermally excited into the conduction band is given by:

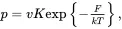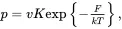(2.1)