It can be shown that the bounds for the effective shear modulus derived by Hashin and Shtrikman [6, Equations ( 3.44)–( 3.50)] and the bounds derived by Walpole [7, Equation (26)] are identical and may be expressed in the following form that has the same structure as the result ( 3.46) derived using Maxwell’s methodology
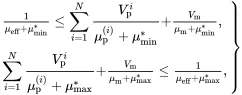 (3.48)
(3.48)
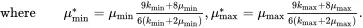 (3.49)
(3.49)
The parameters kmin and μmin are the lowest values of the bulk and shear moduli of all phases in the composite, respectively, whereas kmax and μmax are the highest values. On writing
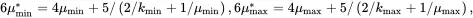 (3.50)
(3.50)
it follows that μmax*≥μmin* for all values of the bulk and shear moduli, indicating that the ‘max’ and ‘min’ subscripts are used in an appropriate sense. It should be noted that kmin and μmin may be associated with different phases, and similarly for kmax and μmax.
3.5 Summary of Results
3.5.1 Multiphase Composites
Key results, ( 3.10) for thermal conductivity, ( 3.27) for bulk modulus and ( 3.46) for shear modulus, derived using Maxwell’s methodology have the following simple common structure, involving ‘mixtures’ formulae for the effective isotropic properties ϕ of the composite
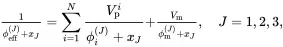 (3.51)
(3.51)
 (3.52)
(3.52)
The inequalities ( 3.12), ( 3.30) and ( 3.48), valid for all volume fractions, lead to rigorous bounds valid for any phase geometries that are statistically isotropic. They have the following common structure that is strongly related to the structure defined by ( 3.51) and ( 3.52) for effective properties determined using Maxwell’s methodology
 (3.53)
(3.53)
 (3.54)
(3.54)
By comparing the bounds ( 3.53) with ( 3.51) when J = 1, the result for thermal conductivity obtained using Maxwell’s methodology is exactly the lower bound for κeff when κmin=κm, and the upper bound when κmax=κm. When κmin<���κm<���κmax, the result for effective thermal conductivity obtained using Maxwell’s methodology lies between the bounds for all volume fractions. A comparison of ( 3.53) with ( 3.51) when J = 2 shows that the result obtained for bulk modulus using Maxwell’s methodology leads exactly to the lower bound for keff when μmin=μm, and the upper bound when μmax=μm. When μmin<���μm<���μmax, the result for effective bulk modulus obtained using Maxwell’s methodology lies between the bounds for all volume fractions. A comparison of ( 3.53) with ( 3.51) when J = 3 shows that the result ( 3.51) obtained for shear modulus using Maxwell’s methodology leads exactly to the lower bound for μeff when μmin*=μm*, and the upper bound when μmax*=μm*. When μmin*<���μm*<���μmax*, the result for effective shear modulus obtained using Maxwell’s methodology lies between the bounds for all volume fractions. Thus, it has been shown that effective thermoelastic properties, obtained above using Maxwell’s methodology, do not lie beyond rigorous bounds for properties for all volume fractions consistent with isotropic effective properties. This characteristic of Maxwell’s methodology provides significant evidence that its validity is not confined to small volume fractions.
3.5.2 Two-phase Composites
When N = 1, it follows from ( 3.2) and ( 3.11) that the result first derived by Maxwell [3] for the analogous case of electrical conductivity is obtained, which may be expressed in the form of a mixtures estimate plus a correction term so that
 (3.55)
(3.55)
It follows from ( 3.28), ( 3.29) and ( 3.47) derived using Maxwell’s methodology, that the effective bulk modulus, thermal expansion coefficient and shear modulus may be expressed as a mixtures estimate plus a correction term, so that
 (3.56)
(3.56)
 (3.57)
(3.57)
 (3.58)
(3.58)
where
 (3.59)
(3.59)
3.6 Bounds for Two-phase Isotropic Composites
It follows from Hashin and Shtrikman [5], and the review by Hashin [1], that bounds for the effective thermal conductivity of a two-phase composite, valid for arbitrary reinforcement geometries leading to statistically isotropic effective properties, may be expressed in the form
 (3.60)
(3.60)
 (3.61)
(3.61)
Walpole [7, Equation (26)] has derived rigorous bounds for the effective bulk modulus, which can for a two-phase composite be expressed in the following two equivalent forms
 (3.62)
(3.62)
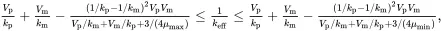 (3.63)
(3.63)
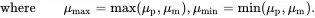 (3.64)
(3.64)
Читать дальше

 (3.48)
(3.48)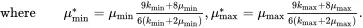 (3.49)
(3.49)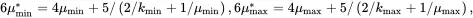 (3.50)
(3.50)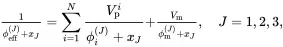 (3.51)
(3.51)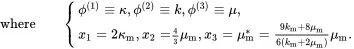 (3.52)
(3.52) (3.53)
(3.53)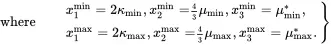 (3.54)
(3.54)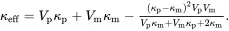 (3.55)
(3.55)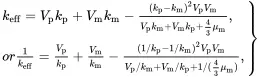 (3.56)
(3.56) (3.57)
(3.57) (3.58)
(3.58)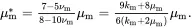 (3.59)
(3.59)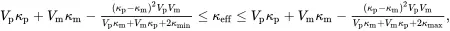 (3.60)
(3.60)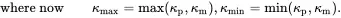 (3.61)
(3.61)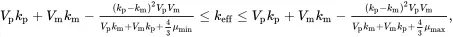 (3.62)
(3.62)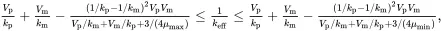 (3.63)
(3.63)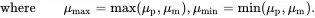 (3.64)
(3.64)










