3.4 Shear Modulus
3.4.1 Spherical Particle Embedded in Infinite Matrix Material Subject to Pure Shear Loading
For a state of pure shear, and in the absence of thermal effects, the displacement field of a homogeneous sample of material referred to a set of Cartesian coordinates (x1,x2,x3) has the form
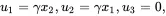 (3.31)
(3.31)
and the corresponding strain and stress components are given by
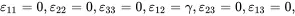 (3.32)
(3.32)
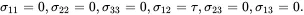 (3.33)
(3.33)
The parameters γ and τ are the shear strain (half the engineering shear strain) and shear stress, respectively, such that τ=2μγ where μ is the shear modulus of an isotropic material. The principal values of the stress field are along (tension) and perpendicular to (compression) the line x2=x1.
A single spherical particle of radius a is now placed in, and perfectly bonded to, an infinite matrix, where the origin of spherical polar coordinates ( r , θ , ϕ ) is taken at the centre of the particle. The system is then subject only to a shear stress applied at infinity. At the particle/matrix interface the following perfect bonding boundary conditions must be satisfied:
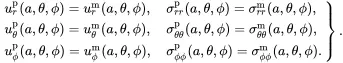 (3.34)
(3.34)
A displacement field equivalent to that used by Hashin [5 ], based on the analysis of Love [8, Equations (5)–(7)] that leads to a stress field satisfying the equilibrium equations and the stress-strain relations ( 3.15) with ΔT=0, can be used to solve the embedded isolated sphere problem (see Appendix A). The displacement and stress fields in the particle are bounded at r = 0 so that
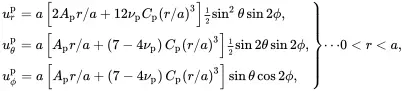 (3.35)
(3.35)
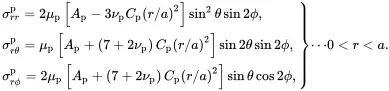 (3.36)
(3.36)
In the matrix the displacement field and stress field (stresses bounded as r→∞) have the form
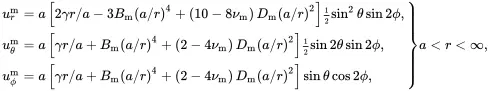 (3.37)
(3.37)
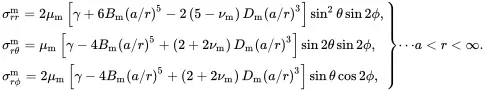 (3.38)
(3.38)
The representation is identical in form to that used by Christensen and Lo [9] although they used a definition of ϕ that differs from that used here by an angle of π/4. This difference has no effect on the approach to be followed. It follows from ( 3.35)–( 3.38) that the continuity conditions ( 3.34) are satisfied if the following four independent relations are satisfied
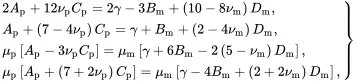 (3.39)
(3.39)
and it can then be shown that
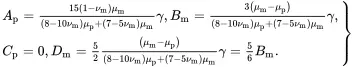 (3.40)
(3.40)
As Cp=0, it follows from ( 3.35) and ( 3.36) that both the strain and stress distributions in the particle are uniform.
3.4.2 Application of Maxwell’s Methodology
To apply Maxwell’s methodology to a cluster of N particles embedded in an infinite matrix, the stress distribution in the matrix at large distances from the cluster is considered. The perturbing effect in the matrix at large distances from the cluster of particles is estimated by superimposing the perturbations caused by each particle, regarded as being isolated, and regarding all particles to be located at the origin. The properties of particles of type i will again be denoted by a superscript (i).
The stress distribution at very large distances from the cluster is then given by the following generalisation of relations ( 3.38)
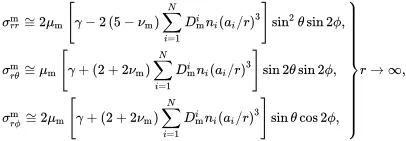 (3.41)
(3.41)
where from ( 3.40), for i = 1, …, N ,
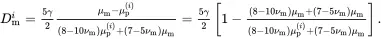 (3.42)
(3.42)
For the isolated sphere of radius b having the effective properties of the particulate composite cluster as illustrated in Figure 3.1(b), it follows that the stress field in the matrix at large distances is described exactly by relations of the type ( 3.38) where the coefficient Dm is replaced by D¯m having the value determined by the relation
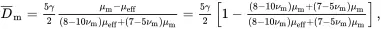 (3.43)
(3.43)
where μeff is the effective shear modulus of the isotropic particulate composite. It then follows from ( 3.38) and ( 3.40) that the exact matrix stress distribution, for a given value of μeff, is
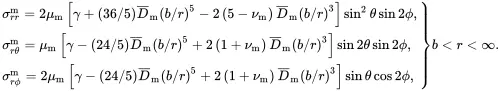 (3.44)
(3.44)
As the stress distribution given by ( 3.41) must be identical at large distances from the cluster with that specified by ( 3.44) it follows, from a consideration of terms proportional to r−3, that
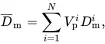 (3.45)
(3.45)
where use has been made of ( 3.1). On substituting ( 3.42) and ( 3.43) into ( 3.45), it can be shown using ( 3.1) that the following ‘mixtures’ result is obtained for the function 1/(μ+μm*)
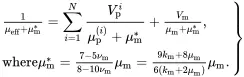 (3.46)
(3.46)
On using ( 3.1), the effective shear modulus may be estimated using the following relation
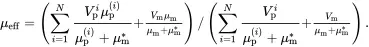 (3.47)
(3.47)
Читать дальше

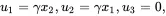 (3.31)
(3.31)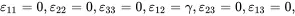 (3.32)
(3.32)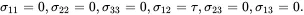 (3.33)
(3.33)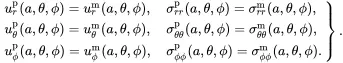 (3.34)
(3.34)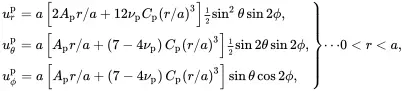 (3.35)
(3.35)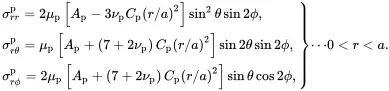 (3.36)
(3.36)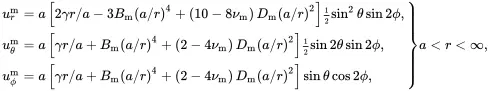 (3.37)
(3.37)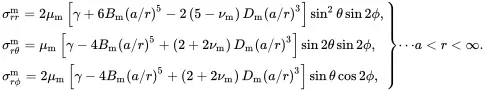 (3.38)
(3.38)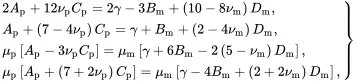 (3.39)
(3.39)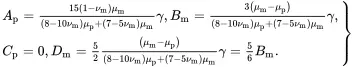 (3.40)
(3.40)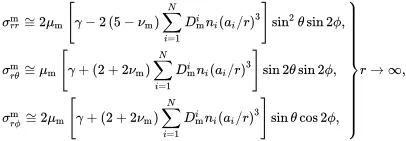 (3.41)
(3.41)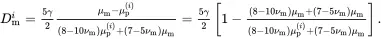 (3.42)
(3.42)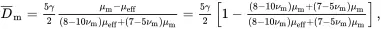 (3.43)
(3.43)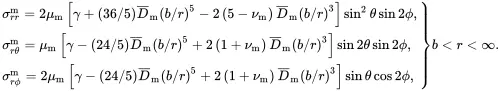 (3.44)
(3.44)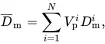 (3.45)
(3.45)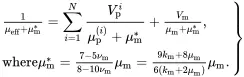 (3.46)
(3.46)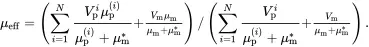 (3.47)
(3.47)










