Andrew Zimmerman Jones - String Theory For Dummies

Waves (as we usually think of them) move through some sort of medium. Like in the examples we discussed when talking about kinetic energy, tidal waves can move through the water, and sound waves through the air, with those materials acting as the medium for the motion. Similarly, if you flick the end of a jump rope or string, a wave moves along the rope or string. In classical physics, waves transport energy, but not matter, from one region to another. One set of water molecules transfers its energy to the nearby water molecules, which means that the wave moves through the water, even though the actual water molecules don’t really travel all the way from the start of the wave to the end of the wave.

This is even more obvious if we take the end of a jump rope and shake it, causing a wave to travel along its length. Clearly, the molecules at our end of the jump rope aren’t traveling along it. Each group of jump-rope molecules is nudging the next group of jump-rope molecules, and the end result is the wave motion along its length.

There are two types of mechanical waves, as shown in Figure 5-1:

Transverse wave: A wave in which the displacement of the medium is perpendicular to the direction of travel of the wave along the medium, like the flicking of a jump rope

Longitudinal wave: A wave that moves in the same direction in which the wave travels, like a piston pushing on a cylinder of water

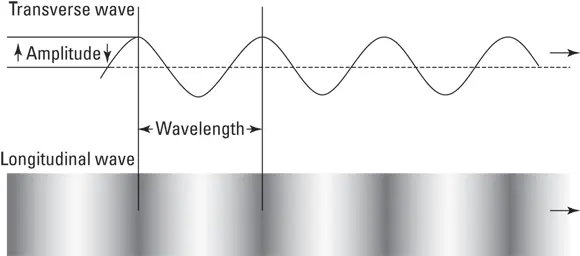
FIGURE 5-1:Waves come in two types: transverse, shown on top, and longitudinal, shown on the bottom.

The highest point on a transverse wave (or the densest point in a longitudinal wave) is called a crest. The lowest point on a transverse wave (or the least dense point in a longitudinal wave) is called a trough.

The displacement from the resting point to the crest — in other words, how high the wave gets — is called the amplitude. The distance from one crest to another (or one trough to another) is called the wavelength. These values are shown on the transverse wave in Figure 5-1. The wavelength is shown on the longitudinal wave as well, although the amplitude is hard to show on that type of wave, so it isn’t included.

Another useful thing to consider is the velocity (speed and direction) of the wave. This can be determined by its wavelength and frequency, which is a measure of how many times the wave passes a given point per second. If you know the frequency and the wavelength, you can calculate the velocity. This, in turn, allows you to calculate the energy contained within the wave.

Another trait of many waves is the principle of superposition, which states that when two waves overlap, the total displacement is the sum of the individual displacements, as shown in Figure 5-2. This property is also referred to as wave interference.

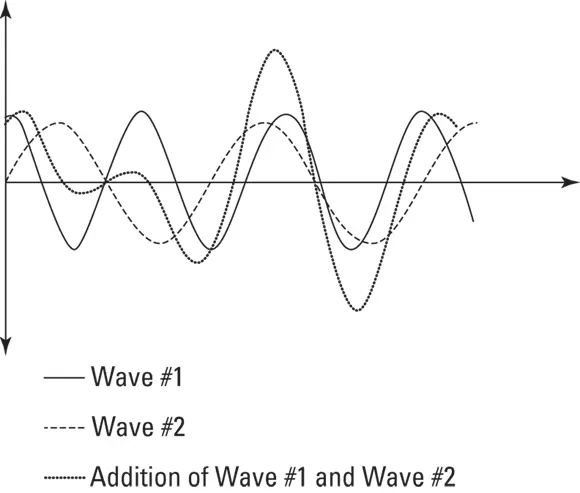
FIGURE 5-2:When two waves overlap, the total displacement is the sum of the two individual displacements.

Consider waves when two ships cross each other’s path. The waves made by the ships cause the water to become choppier, and as the waves add height to each other, they cause massive swells.

Similarly, sometimes waves can cancel each other out. If the crest of wave 1 overlaps with the trough of wave 2, they cancel each other out at that point. This sort of interference plays a key role in one of the quantum physics problems we discuss in Chapter 7— the double slit experiment.

String theory depicts strings of energy that vibrate, but the strings are so tiny that you never perceive the vibrations directly, only their consequences. To understand these vibrations, you have to understand a classical type of wave called a standing wave — a wave that doesn’t appear to be moving.

In a standing wave, certain points, called nodes, don’t appear to move at all. Other points, called antinodes, have the maximum displacement. The arrangement of nodes and antinodes determines the properties of various types of standing waves.

The simplest example of a standing wave is one with a node on each end, such as a string that’s fixed in place on the ends and plucked. When there is a node on each end and only one antinode in between them, the wave is said to vibrate at the fundamental frequency.

Consider a jump rope that is held at each end by a child. The ends of the rope represent nodes because they don’t move much. The center of the rope is the antinode, where the displacement is the greatest and where another child will attempt to jump in. This is vibration at the fundamental frequency, as demonstrated in Figure 5-3a.

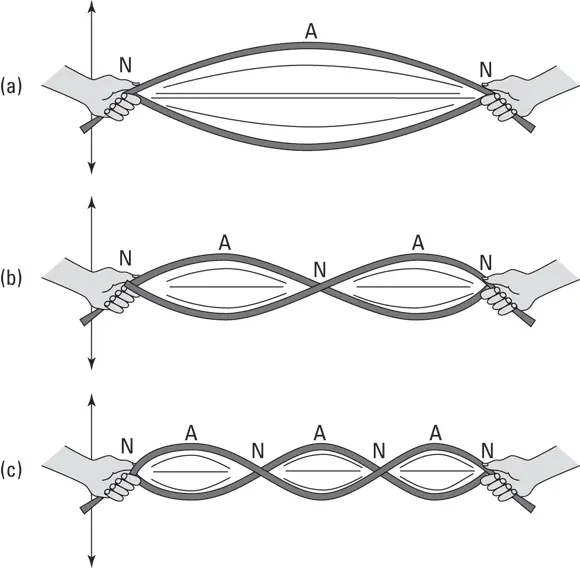
FIGURE 5-3:Examples of standing waves, demonstrating the first three normal modes of a string fixed at both ends. The top wave represents the fundamental frequency.

If the children get ambitious, however, and begin putting more energy into the wave motion of their jump rope, a curious thing happens. Eventually, the children will pump enough energy into the rope that instead of one large antinode, two smaller antinodes are created, and the center of the rope seems to be at rest, as shown in Figure 5-3b. It’s almost as if someone grabbed the middle of the rope and is gingerly, but firmly, holding it in place! (If you are a musician, you may recognize this as the second harmonic or first overtone of the rope.)

Another type of standing wave can be considered if instead of a child holding each end of the rope, one end is mounted on a ring around a pole. The child holding one end begins the wave motion, but the end on the pole is now unconstrained and moves up and down. Instead of having a node on each end, one end is a node (held by the child), and the other is an antinode (moving up and down on the pole).

A similar situation happens when a musician uses a pipe that’s closed at one end and open at the other, like pipes in an organ. A node forms at the closed end of the pipe, but the open end of the pipe is always an antinode.

A third type of standing wave has an antinode at each end. This would be represented by either a pipe that’s open on both ends or a rope that’s free to move on both ends.

The more energy that’s pumped into the standing wave, the more nodes form (see Figure 5-3c). The series of frequencies that cause new nodes to form are called harmonics or, in music, overtones. The waves that correspond to harmonics are called normal modes or vibrational modes.

Music works because of the manipulation and superposition of harmonic overtones created by these normal modes of vibration. The first three normal modes are shown in Figure 5-3, where a string is fixed on both ends.

In string theory, the vibrational modes of strings (and other objects) are similar to the vibrating waves that we are talking about in this chapter. In fact, matter itself is seen as the manifestation of standing waves on strings. Different vibrational modes give rise to different particles! We perceive the particles from the lowest vibrational modes, but with higher energies, we may be able to detect other, higher-energy particles.