Маркус дю Сотой - О том, чего мы не можем знать. Путешествие к рубежам знаний

Можно ли использовать эту стратегию для продления нашей конечной жизни? Могу ли я обмануть свой собственный период полураспада? Проблема состоит в том, что, как я уже объяснял, на моем стремительном космическом корабле одновременно замедляется все. Разгон до околосветовой скорости не позволит мне выжать из Вселенной никакого дополнительного времени, чтобы решить наконец те задачи, над которыми я работаю, потому что, хотя мое тело и будет стареть медленнее, срабатывание моих нейронов замедлится тоже. В соответствии с принципом относительности мне будет казаться, что сам я неподвижен, а стремительно движется все остальное.

Согласно идеям, высказанным Эйнштейном в 1905 г., время, которое я вижу на своих часах, оказалось гораздо более текучим, чем мы предполагали. Абсолютный характер времени во Вселенной станет еще более сомнительным, если задуматься о том, что означает одновременность двух событий. Именно с этой проблемой столкнулся Эйнштейн, когда работал с патентами по синхронизации времени. Оказывается, такой вопрос просто не имеет смысла. Или по меньшей мере ответ на него зависит от системы отсчета.

Начнем со сцены из воображаемого фильма под названием «Относительные псы» – в честь Тарантино [86]. В разных концах поезда стоят два человека с одинаковыми пистолетами. Точно посередине между ними находится третий член банды. Поезд проезжает мимо станции. Эту сцену наблюдает стоящий на станции полицейский. Рассмотрим сначала, что происходит в поезде. С точки зрения бандитов, поезд можно считать неподвижным. Пистолеты стреляют. Обе пули попадают в человека, стоящего посередине, одновременно. Скорости пуль и расстояния, которые они должны пролететь, одинаковы, и, с точки зрения всех пассажиров поезда, оба стрелка нажимают на спуск в один и тот же момент. Более того, жертва видит две вспышки света, вырывающиеся из стволов в один и тот же момент – непосредственно перед тем, как в нее попадают пули.

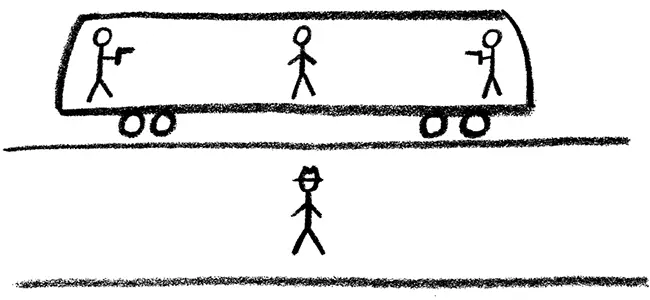
А что происходит с точки зрения полицейского? Предположим, что жертва проезжает мимо полицейского в точности в тот момент, когда обе световые вспышки достигают жертвы, так что полицейский видит эти вспышки в тот же самый момент. Но тут у него возникают сомнения: какое расстояние прошел этот свет? Хотя сейчас оба пистолета находятся от него на одинаковом расстоянии, в момент выстрела пистолет, находящийся в голове поезда, был к нему ближе. Поэтому свет, вышедший из него, должен был пройти более короткое расстояние, чем свет, испущенный из хвоста поезда. А в таком случае, поскольку скорость света постоянна, если обе вспышки достигли цели в один и тот же момент, свет, пришедший из хвоста поезда, должен был выйти из пистолета раньше, чем другая вспышка вылетела из пистолета в голове поезда. Итак, полицейскому кажется, что стрелок, стоящий в хвосте поезда, выстрелил раньше. Но, если поместить еще одного полицейского на поезд, идущий в обратном направлении, ситуация будет обратной, и второй полицейский заключит, что первым должен был выстрелить пистолет, находящийся в голове поезда [87].

Так кто же выстрелил первым? С точки зрения полицейского, стоящего на платформе, – стрелок, находящийся в хвосте поезда, а с точки зрения полицейского, едущего на встречном поезде, – другой стрелок, находящийся в голове. Поэтому разговор о том, какой пистолет выстрелил первым, в абсолютном выражении смысла не имеет. Время принимает разные значения в разных системах отсчета. Оказывается, однако, что существует нечто, абсолютное для всех наблюдателей, но, чтобы его получить, необходимо объединить время и пространство.

Проблема состоит в том, что мы пытаемся измерить расстояние между двумя объектами, а оно изменяется в зависимости от нашего движения относительно этих двух точек. Точно так же изменяется и время, разделяющее два события. Но, если ввести новое определение расстояния, которое определяет расстояние во времени и в пространстве, можно получить нечто инвариантное, то есть независимое от измеряющего. Автор этой великой идеи – Герман Минковский, бывший некогда учителем Эйнштейна в Цюрихском политехникуме. Услышав об идеях Эйнштейна, он немедленно понял, что идеальной сценой для теории Эйнштейна должны быть те многомерные геометрии, которые открыл за полвека до того немецкий математик Бернхард Риман.