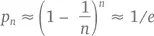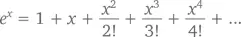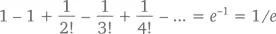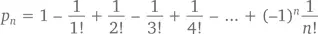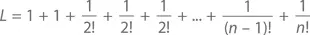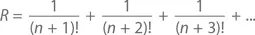Артур Бенджамин - Магия математики - Как найти x и зачем это нужно

Одна из самых моих любимых задач, связанных с вероятностью, – задача о сочетании пар . Представьте себе класс, состоящий из n учеников. Учитель раздает им тетрадки с проверенным домашним заданием. Но то ли по рассеянности, то ли от усталости раздает он их как попало, в случайном порядке (то есть тетрадка может попасть как к своему хозяину, так и к любому другому ученику). Каков шанс того, что ни одна из тетрадок не попадет в «правильные» руки? Иными словами, если мы возьмем все числа от 1 до n и «перемешаем» их в произвольном порядке, какова вероятность того, что ни одно из них не совпадет со своей «правильной» позицией? Например, при n = 3 чи́сла 1, 2 и 3 можно «перемешать» 3! = 6 разными способами, но под наши условия подходят только два из них: 231 и 312. Следовательно, для n = 3 нужная нам вероятность составит 2 к 6 или 1 к 3.

С количеством тетрадей, равным n , существует n ! возможных способов распределения их между учениками. Количество тех из них, которые соответствуют нашим условиям, обозначим как D n . Тогда шанс того, что никто из учеников не получит свою тетрадку, составит p n = D n / n !. Если n равно 4, то D nбудет равно 9:

И тогда p 4= D 4/4! = 9/24 = 0,375.

А вот каковы вероятности для других значений n :

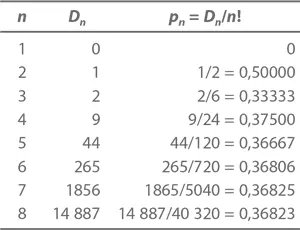
С увеличением n значение pn будет все ближе и ближе подбираться к 1/ e . И вот что самое удивительное: вероятность попадания тетрадок в руки их законных хозяев совершенно не зависит от количества учеников в классе, будь их десять, сто или миллион. И вероятность эта эти очень-очень близка к величине 1/ e .

Но откуда берется это 1/ e ? В первом нашем представлении, с числом учеников, равным n , возможность каждого из них получить свою тетрадь составляет 1/ n , а возможность получить чужую – 1 – (1/ n ). Возьмем последнюю величину и распространим ее на весь класс:

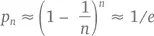
Почему приблизительно, спросите вы? Да потому что здесь, в отличие от задачи с лотерейными билетами, мы не сталкиваемся с последовательностью независимых друг от друга событий. Количество тетрадок ограничено, поэтому первое же «попадание» учителя в цель немного увеличит шансы второго ученика получить чужую тетрадку (то есть вместо 1/ n мы будем иметь уже 1/( n – 1)), а первый же «промах» – немного уменьшит. Но так как и в том и в другом случае вероятность изменяется незначительно, на верности нашего представления это не слишком сказывается.

Точное же значение p n основывается на бесконечной последовательности для e x :

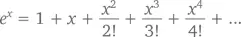
Если в этом уравнении мы подставим x = –1, у нас получится

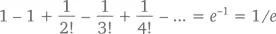
То есть в классе, состоящем из n учеников, вероятность того, что никто из них не получит свою тетрадь, составляет ровно

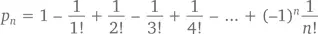
Например, если n = 4, p n= 1 – 1 + 1/2 – 1/6 + 1/24 = 9/24 – ответ, к которому мы уже приходили выше. Приближение к 1/ e здесь невероятно стремительно. Промежуток между p nи 1/ e меньше, чем 1/( n + 1)!. Следовательно, значение p 4находится в диапазоне от 1/5! = 0,0083 до 1/ e , значение p 10совпадает с 1/ e вплоть до 7 знаков после запятой, а значение p 100 – вплоть до 150 знаков!

Теорема:Число e является иррациональным.

Доказательство:Предположим обратное – что число e является рациональным. Тогда при положительных целых значениях m и n будет верно то, что e = m / n . С помощью n разобьем бесконечную последовательность для e на две части – так, чтобы e было равно L + R , то есть

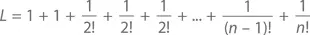
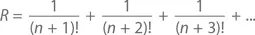
Обратите внимание, что n!e = en ( n– 1)! = m ( n– 1)! должно быть целой величиной (потому что и m , и ( n – 1)! суть целые величины), равно как и n!L (потому что n !/ k ! есть целая величина при любом k ≤ n ). Следовательно, n!R = n!e – n!L представляет собой разность двух целых чисел, а значит, и само является целым числом, что невозможно: поскольку условие, что n ≥ 1, означает, что