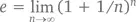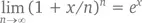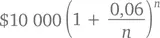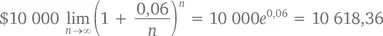Артур Бенджамин - Магия математики - Как найти x и зачем это нужно

3. Прибавьте к нему единицу.

4. Возведите результат в степень, равную загаданному семизначному числу (нажимаете кнопку x y , вводите семь цифр и нажимаете «равно»).

Первые четыре цифры ответа – 2,718, да? Не удивлюсь даже, если у вас получится

то есть цифр, совпадающих с иррациональным числом e , будет куда больше.

Так что это за мистическое e такое, в чем его секрет и зачем оно вообще нужно?

Ваши операции с калькулятором свелись, по сути, к

где n и есть ваше семизначное число. Семь знаков – много, но что будет, если их будет еще больше? С одной стороны, число (1 + 1/ n ) будет все ближе и ближе подбираться к единице, которая при возведении в степень останется единицей. Следовательно, было бы разумным предположить, что при любом большом значении n (1 + 1/ n ) nбудет приблизительно равно единице (например, 1,001 100≈ 1,105).

С другой стороны, даже при больших значениях n результат (1 + 1/ n ) никогда не опустится ниже этой самой единицы. А при последовательном возведении такого числа во все бо́льшую и бо́льшую степень, увеличиваться будет и итог (скажем, 1,001 10 000будет больше 20 000).

Сложность здесь заключается в том, что «основа» (1 + 1/ n ) становится тем меньше , чем больше возрастает n . И это постоянное «перетягивание каната» между единицей и бесконечностью пододвигает ответ все ближе и ближе к e = 2,71828… (Так, 1,001 1000≈ 2,717.)

Давайте посмотрим повнимательнее, как ведет себя функция (1 + 1/ n ) nпри возрастающих значениях n :

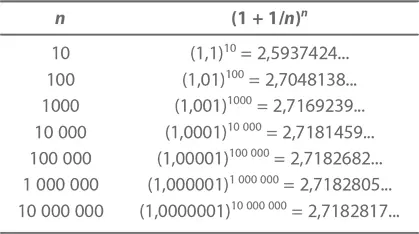
Именно так и определяется число e : как величина, к которой приближается (1 + 1/ n ) n с возрастанием значения n . Математики называют ее пределом (1 + 1/ n ) n при n , стремящейся к бесконечности. Записывается это следующим образом:

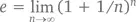
Если заменить дробь 1/ n на x / n , оговорившись, что x есть действительная величина, то с возрастанием n / x число (1 + x / n ) n/x будет все больше приближаться к e . Возведя обе части этого уравнения в степень x (и вспомнив, что ( a b ) c = a bc ), мы приходим к экспоненциальной формуле:

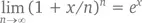
где х – любое комплексное число. Вы удивитесь, но от этой формулы есть вполне себе практическая польза. Предположим, что вы открыли в банке накопительный счет под 6 % годовых (то есть ставка составит 0,06) и положили на него $10 000. Если процент начисляется раз в год, то через 365 дней у вас будет $10 000(1,06) = $10 600. Именно от этой суммы банк будет исчислять 6 % в следующем году: $10 000(1,06)² = $11 236. Через три года уравнение преобразуется в $10 000(1,06)³ = $11 910,16. Через t же лет – в

Чтобы отследить общую закономерность, заменим ставку 0,06 ставкой r , а начальную сумму $10 000 суммой $ P . Тогда через t лет вы смогли бы получить

Теперь предположим, что проценты начисляются дважды в год: по 3 % каждые 6 месяцев. Через год на вашем счете будет лежать $10 000(1,03)² = $10 609 – немного больше, чем в прошлом случае.

С ежеквартальными (раз в три месяца) начислениями вы заработаете 4 раза по 1,5 %, то есть $10 000(1,015) 4= $10 613,63.

Давайте обобщим и это: при начислении процента n раз в год через 365 дней сумма ваших накоплений составит

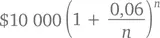
При очень больших значениях n мы будем иметь дело с непрерывными начислениями процента. Согласно второму замечательному пределу, за год получится

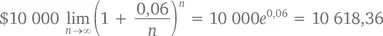
Сведем все это в таблицу:

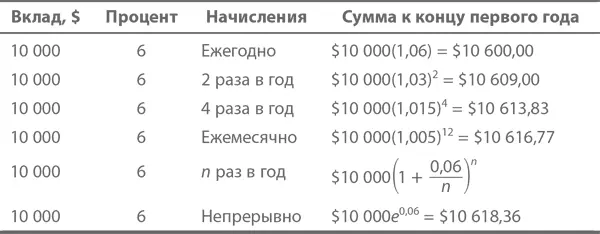
Иными словами, начав с $ P , с непрерывными начислениями по ставке r через t лет вы получите $ A . Все это выражается очень симпатичной во всех отношениях формулой

Как хорошо видно на графике, функция y = e xрастет очень быстро. По соседству с ней мы изобразим графики e 2xи e 0,06x. Правда, похожи? Подобный рост называется ростом по экспоненте . Если же взять график y = e –x, то он очень быстро приближается к 0, то есть демонстрирует спад по экспоненте .