Артур Бенджамин - Магия математики - Как найти x и зачем это нужно

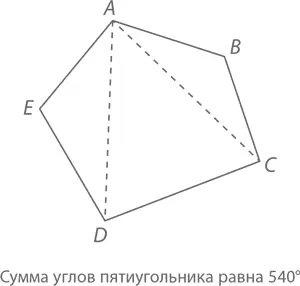
Этот алгоритм можно применять снова и снова, к любому полигону, вплоть до n -угольника.

Здесь отлично сработает метод индукции: для этого надо разделить наш n -угольник на n – 2 треугольников, поэтапно соединяя линиями вершину A со всеми остальными.

Теорема:сумма углов n-угольника равна 180( n – 2) градусам.

А теперь… просто следите за волшебной палочкой! Начертите восьмиугольник (восьмисторонний полигон) и поставьте внутри него 5 точек – где угодно. А теперь соедините их с вершинами углов и друг с другом так, чтобы у вас получались треугольники (именно треугольники – никаких других фигур). Процесс этот называется триангуляцией, и вот несколько его примеров. (Последний восьмиугольник я оставил пустым, чтобы вы могли проделать это сами.)

В обоих моих примерах восьмиугольники разбиты ровно на 16 треугольников. Столько же должно получиться у вас в третьем октагоне вне зависимости от того, где именно вы поставили 5 точек. (А если вдруг нет, значит, вы где-то ошиблись – в этом случае просто внимательно приглядитесь к каждой доле и убедитесь, что в ней ровно 3 точки, а не 4; если же их все-таки 4, проведите линию от одного угла доли к другому, чтобы разделить ее на два треугольника.) Объяснить это можно с помощью следующей теоремы.

Теорема:В процессе триангуляции n -сторонний полигон, имеющий внутри некое количество точек, равное p , будет разделен ровно на 2 p + n – 2 треугольников.

В нашем предыдущем примере n = 8, а p = 5, поэтому треугольников получается 10 + 8 – 2 = 16.

Доказательство:Предположим, что в процессе триангуляции у нас получается количество треугольников, равное T . Мы можем доказать, что T = 2 p + n – 2, решив одну арифметическую задачку двумя разными способами. Итак, внимание!

Вопрос: Чему будет равна сумма углов всех треугольников?

Ответ 1: Так как количество треугольников равно T , а сумма углов каждого из них – 180°, общая сумма составит 180 T градусов.

Ответ 2: Разобьем задачу на две. Углы, прилежащие к каждой из внутренних точек (напомним, что их количество равно p ), образуют окружность, следовательно, их общая сумма составит 360 p градусов. С другой стороны, из предыдущей теоремы мы знаем, что сумма углов n -угольника равна 180( n – 2) градусам. Значит, всего получится 360 p + 180( n – 2) градусов.

Из двух ответов составим уравнение

Разделим обе части на 180, что даст нам

что и требовалось доказать.☺

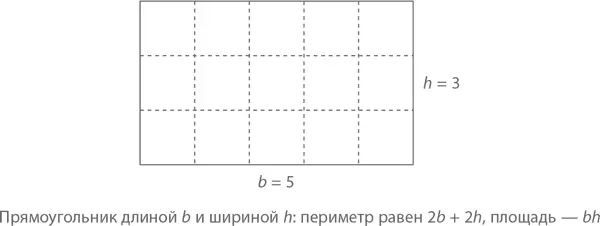
Периметр полигона есть сумма длин его сторон. Так, периметр прямоугольника длиной b и шириной h будет равен 2 b + 2 h , потому что и b , и h суть размеры каждой из двух его сторон. А как насчет площади? Исходим из того соображения, что площадь квадрата размером 1 на 1 (так называемого единичного квадрата) равна 1. При положительных целых значениях b и h (как на рисунке) мы можем разбить всю площадь на bh единичных квадратов, а значит, она будет равна bh . В целом же, любой прямоугольник с длиной b и шириной h (где b и h суть положительные, но необязательно целые величины) имеет площадь bh .

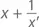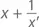В этой главе мы уже не раз обращались к помощи алгебры, чтобы разрешить исключительно геометрические проблемы. Принцип этот прекрасно работает и в обратную сторону: порой геометрия значительно облегчает понимание алгебры. Взгляните на типичную задачу. Насколько малым может быть значение где x есть любое положительное число? При x = 1 имеем 2, при x = 1,25 – 1,25 + 0,8 = 2,05, при x = 2 – 2,5. Логика подсказывает, что наименьшим ответом будет 2, и это на самом деле так, только вот как нам в этом удостовериться? Самый простой и эффективный метод расчета будет предложен в главе 11, пока же давайте ограничимся методом геометрическим.