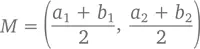Артур Бенджамин - Магия математики - Как найти x и зачем это нужно

Теорема:треугольник XYP имеет наименьший периметр, если точка P , которая расположена на прямой, параллельной его основанию, находится точно в середине отрезка XY .

И хотя для того, чтобы подтвердить это предположение, достаточно пары нехитрых вычислительных операций, побалуем себя изысканным геометрическим подходом (доказательство получится очень долгим и немного запутанным, поэтому, если хотите, можете особо в него не вчитываться, а то и вовсе пропустить).

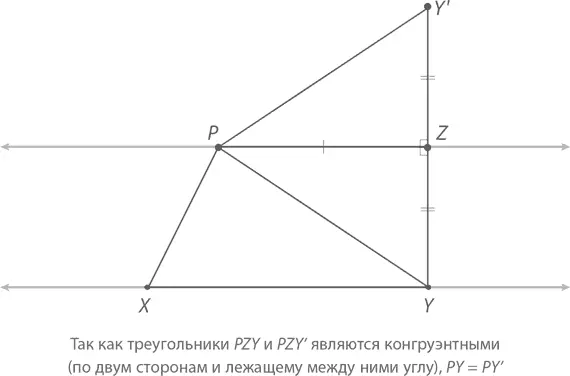
Доказательство:Предположим, что точка P располагается абсолютно в любом месте на верхней прямой, а точка Z располагается прямо над точкой Y . (Точнее говоря, точка Z должна быть расположена так, чтобы линия YZ , проведенная от нее в точку Y , была строго перпендикулярна как нижней, так и верхней прямым, как показано на рисунке чуть ниже.) Продолжим линию YZ до точки Y ´так, чтобы отрезок Y ´ Z был равным отрезку ZY . Другими словами, если бы верхняя прямая была зеркалом, точка Y ´ была бы отражением точки Y .

Треугольники PZY и PZY ´ будут конгруэнтными согласно аксиоме по двум сторонам и лежащему между ними углу: PZ = PZ , ∠ PZY = 90° = ∠ PZY ´, а ZY = ZY ´. Следовательно, PY = PY ´, из чего и будем исходить далее.

Периметр треугольника YXP есть сумма длин трех отрезков:

а так как мы только что доказали, что PY = PY ´, тот же периметр можно представить в виде

Длина YX не зависит от P , так что задачу по поиску ее местонахождения можно упростить до поиска наименьшего значения XP + PY ´.

Отрезки XP и PY образуют ломаную линию, которая соединяет точки X и Y ´. Но так как наиболее кратким путем между двумя точками будет не ломаная, а прямая линия, в оптимальном варианте точка P * должна располагаться на одной прямой с точками X и Y ´, причем на месте ее пересечения с верхней горизонталью, как на рисунке ниже. Все? Нет, еще не все: нам же нужно доказать, что P * находится точно над центральной точкой отрезка XY .

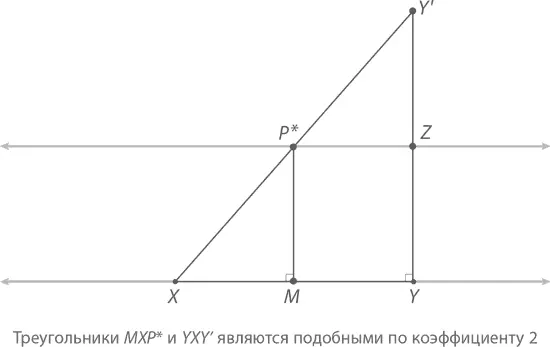
Обозначим точку, находящуюся прямо под точкой P * буквой M . Отрезок P*M при этом будет перпендикулярен XY . Так как верхняя прямая параллельна нижней, длина P * M должна быть равна длине ZY . В принципе, это понятно и так, ведь расстояние между двумя параллельными прямыми равно всегда – хоть на видимом участке, хоть в бесконечности, – но дополнительным подтверждением тому является отрезок MZ , который дает нам два конгруэнтных (согласно теореме – по двум углам и прилежащей к одному из них стороне) треугольника MYZ и ZP * M .

Чтобы доказать, что точка M лежит ровно в центре отрезка XY , докажем сначала подобность треугольников MXP * и YXY ´. Обратите внимание, что ∠ MXP * и ∠ YXY ´ суть один и тот же угол, ∠ P * MX = ∠ Y ´ YX , так как они оба прямые, а раз мы имеем полное совпадение в двух парах углов, совпасть должны углы и в третьей паре, чтобы в каждом треугольнике получилось по 180°. Каким будет масштабирующий коэффициент? Согласно построению,

поэтому масштабирующий коэффициент будет равен 2. Следовательно, длина XM составляет ровно половину от длины XY , а отрезок XM заканчивается ровно в центре отрезка XY .

Обобщая, мы можем утверждать, что для того, чтобы треугольник XYP имел наименьший периметр, точка P* верхней прямой должна располагаться точно над центральной точкой отрезка XY .◻

Порой геометрические задачи можно решить с помощью алгебры. Предположим, например, что отрезок AB лежит на поверхности с координатами ( a 1, a 2) для точки A и координатами ( b 1, b 2) для точки B . Тогда точка M , располагающаяся в середине этого отрезка, будет иметь координаты

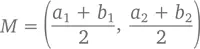
как показано на графике. То есть если, скажем, A = (1, 2), а B = (3, 4), центром отрезка AB является точка M = ((1 + 3)/2, (2 + 4)/2) = (2, 3).