Артур Бенджамин - Магия математики - Как найти x и зачем это нужно

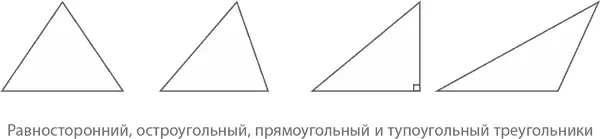
Теорема о равнобедренном треугольнике:Если в равнобедренном треугольнике ABC стороны AB и AC равны, противолежащие этим сторонам углы будут также равны.

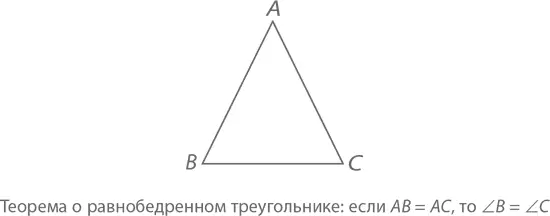
Доказательство:Из точки A проведем линию так, чтобы она делила ∠ A ровно пополам и пересекала отрезок BC в точке X , как на рисунке. Это биссектриса угла A .

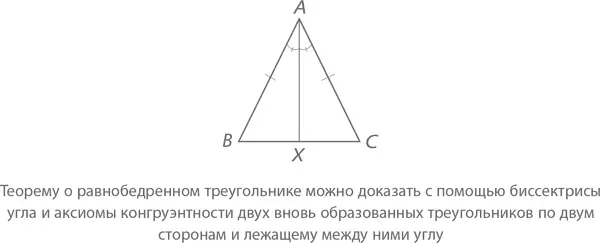
Получившиеся таким образом треугольники BAX и CAX являются конгруэнтными согласно аксиоме по двум сторонам и лежащему между ними углу: BA = CA (что следует из понятия равнобедренности), ∠ BAX = ∠ CAX (что следует из понятия биссектрисы), а AX = AX (вернее, не так: отрезок AX не уникален, он появляется одновременно в двух треугольниках и не меняет свою длину). А так как BAX ≅ CAX, также равны будут и остальные стороны и углы, в том числе ∠B = ∠C, что и требовалось доказать.◻

То же можно доказать и с помощью теоремы конгруэнтности по трем сторонам. Для этого возьмем точку M как середину отрезка BC , то есть чтобы BM было равно MC . Проведем линию по отрезку AM . Как и в предыдущем доказательстве, треугольники BAM и CAM будут конгруэнтными, потому что BA = CA (равнобедренность), AM = AM , а MB = MC (потому что точка M находится ровно посередине BC ). Следовательно, согласно доказательству по трем парам сторон, BAM ≅ CAM , что говорит нам о равности лежащих в них углов, в том числе и ∠ B = ∠ C , что и требовалось доказать.

Из факта конгруэнтности следует, что ∠ BAM = ∠ CAM , следовательно, отрезок AM является биссектрисой. Более того, так как ∠ BMA = ∠ CMA и в сумме они дают 180°, каждый из них должен быть равен 90°, из чего следует вывод, что в равнобедренном треугольнике биссектриса, проложенная из угла A , будет перпендикуляром к основанию BC .

Кстати, доказательство от обратного в отношении равнобедренного треугольника тоже вполне эффективно, то есть если ∠ B = ∠ C , то AB = AC . Для этого, как и в самом первом доказательстве, проведем биссектрису из точки A в точку X . Утверждение, что BAX ≅ CAX , в этом случае следует из теоремы конгруэнтности по двум углам и прилежащей к одному из них стороне: ∠ B = ∠ C (согласно изначальному условию), ∠ BAX = ∠ CAX (согласно определению биссектрисы), а AX = AX . Значит, AB = AC , то есть треугольник ABC является равнобедренным.

Теорему эту можно применить и к равностороннему треугольнику: если равны все стороны, значит, равны и все углы. Следовательно, поскольку в сумме своей три угла дают 180°, имеем сопутствующую теорему.

Сопутствующая теорема:В равностороннем треугольнике каждый из углов равен 60°.

Согласно теореме конгруэнтности по трем сторонам, если в треугольниках ABC и DEF совпадают все стороны (то есть AB = DE, BC = EF , а CA = FD ), их углы будут также совпадать (то есть ∠ A = ∠ D , ∠ B = ∠ E , а ∠ C = ∠ F ). Верным ли будет обратное предположение, что, если в треугольниках ABC и DEF совпадают все углы, будут совпадать и их стороны? Конечно же, нет – просто посмотрите на рисунок:

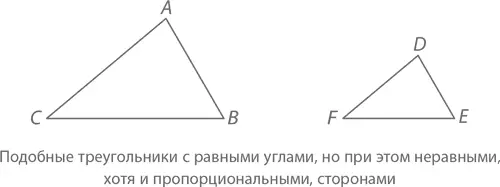
Два треугольника с равными углами называются подобными . Если треугольники ABC и DEF являются подобными (что обозначается как ∆ ABC ~ ∆ DEF или просто ABC ~ DEF ), то ∠ A = ∠ D , ∠ B = ∠ E , а ∠ C = ∠ F . То есть один из них, по сути, является уменьшенной (или увеличенной) версией второго. Поэтому при ABC ~ DEF их стороны находятся в пропорциональной зависимости друг от друга по некоторому положительному масштабирующему коэффициенту k: DE = kAB, EF = kBC , а FD = kCA .

Все это поможет нам ответить на второй вопрос нашей викторины, с которой мы начали главу. Давайте вспомним все условия. У нас есть две параллельные прямые: на нижней пролегает отрезок XY , на верхней – точка P . Нашей задачей было найти такое местоположение точки P , при котором треугольник XYP имел бы наименьший периметр. Преобразуем правильный ответ в теорему.