Артур Бенджамин - Магия математики - Как найти x и зачем это нужно

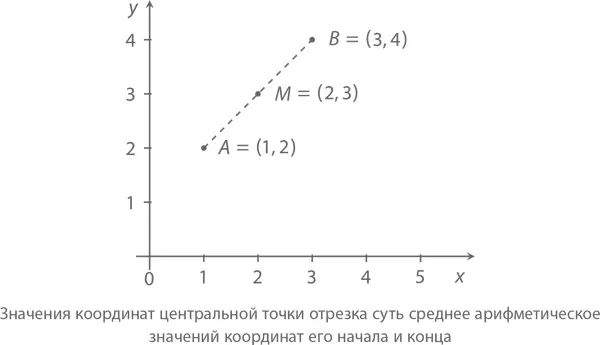
За этим кроется один полезный факт о треугольниках. Начертите треугольник и соедините друг с другом центральные точки любых двух его сторон. Видите, что получается? Ответ кроется в следующей теореме.

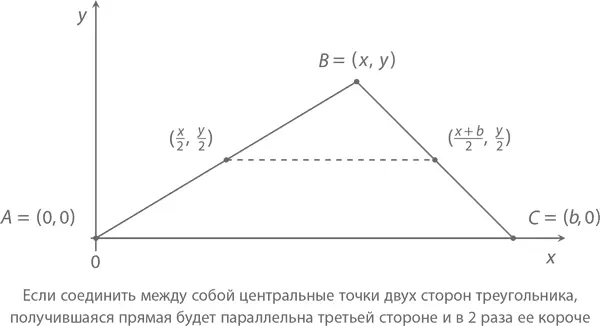
Теорема о центральных точках треугольника:В треугольнике ABC линия между центральной точкой стороны AB и центральной точкой стороны BC будет параллельна стороне AC . Более того, при длине стороны AC , равной b , длина отрезка, соединяющего центральные точки двух других сторон, будет равна b /2.

Доказательство:Поместим треугольник ABC на плоскость так, чтобы точка A располагалась в координатах (0, 0), сторона AC была строго горизонтальной, а точка C , таким образом, имела координаты ( b , 0), как показано на рисунке ниже. Обозначим координаты точки B как ( x, y ). Тогда центральная точка отрезка AB будет находиться в координатах ( x /2, y /2), а центральная точка отрезка BC – в координатах (( x + b )/2, y /2). Так как у них одни и те же y -координаты, соединяющая их линия должна быть строго горизонтальна, то есть параллельна стороне AC . Более того, длина этой линии составит ( x + b )/2 – x /2 = b /2, что и требовалось доказать.

Теорема о центральных точках треугольника поможет нам разгадать фокус, с которого начиналась эта глава: тогда мы взяли четырехугольник ABCD и соединили центральные точки его сторон так, что образовался еще один четырехугольник, EFGH , который оказался (и всегда окажется) параллелограммом. Давайте разберемся, почему так происходит. Диагональная линия, проведенная от вершины A к вершине C , образует два треугольника ABC и ADC (см. рисунок).

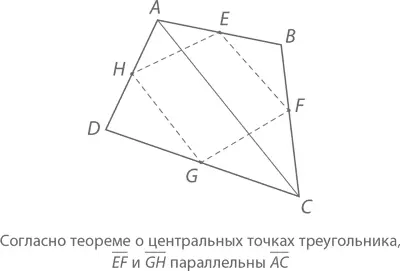
Применив теорему о центральных точках треугольника, мы обнаружим, что отрезок EF будет параллелен отрезку AC , который в свою очередь будет параллелен отрезку GH . Следовательно, EF будет параллельна GH . (Более того, EF и GH будут иметь одинаковую длину, равную половине AC .)

Проведем точно такую же диагональ из вершины B к вершине D и увидим, что FG и HE также параллельны и равны по длине. Следовательно, EFGH является параллелограммом.

Большинство из разобранных нами теорем связано с треугольниками, что ничуть не удивительно, ведь в геометрии этой фигуре уделяется много внимания. Кстати сказать, треугольник есть не что иное, как наипростейшая разновидность полигонов (многоугольников). Дальше идут четырехугольник (четырехсторонний полигон), пятиугольник (пятисторонний полигон) и так далее. Полигон, количество сторон которого равно n , иногда называется n -угольником. Мы уже доказывали, что сумма всех углов треугольника равна 180°. А что насчет остальных полигонов? Любой четырехугольник, будь то квадрат, прямоугольник или параллелограмм, имеет четыре стороны. В прямоугольнике, как явствует из его названия, все 4 угла являются прямыми, то есть равными 90°, а значит, составляют в сумме 360°.

Следующая наша теорема будет верна для любого четырехугольника.

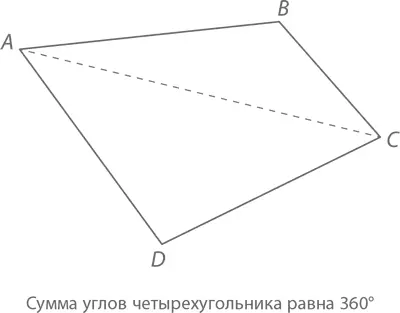
Теорема:Сумма углов четырехугольника равна 360°.

Доказательство:Возьмем любой четырехугольник с вершинами A, B, C и D (вроде того, что изображен на рисунке). Из угла A в угол C проведем линию так, чтобы она разделила четырехугольник на 2 треугольника, сумма углов каждого из которых равна 180°. Следовательно, сумма углов четырехугольника составит 2 × 180° = 360°

Чтобы проследить общую закономерность, разберем еще одну теорему.

Теорема:Сумма углов пятиугольника равна 540°.

Доказательство:Возьмем пятиугольник с вершинами A, B, C, D и E (вроде того, что изображен на рисунке). Линия, проведенная от вершины A к вершине C , разделит пятиугольник на четырех– и треугольник. Сумма углов треугольника ABC составляет 180° (это мы знаем уже давно), сумма углов четырехугольника ACDE – 360° (это мы доказали только что). Следовательно, сумма углов пятиугольника – 180° + 360° = 540°.