Артур Бенджамин - Магия математики - Как найти x и зачем это нужно

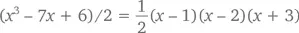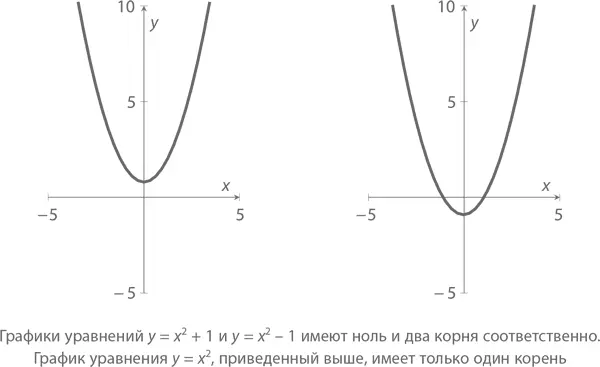
А вот графики двух кубических многочленов, на которых вы легко заметите, что в обоих – максимум три корня.

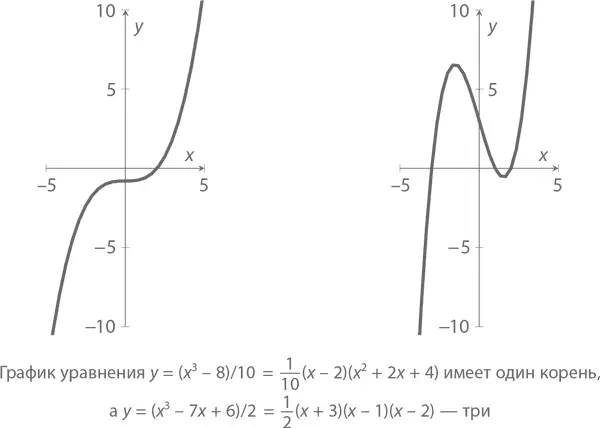
В главе 10 мы рассмотрим основную теорему алгебры , которая гласит, что каждый многочлен, возведенный в степень n , имеет не более n корней. Более того, он может быть разложен на линейную и квадратную части. Например,

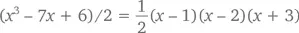
имеет три корня (1, 2 и –3). В свою очередь,

имеет только один действительный корень – при x = 2 (и еще два комплексных , но им придется подождать до главы 10). Сегодня, кстати, очень легко можно найти график практически любой функции, просто набрав нужное вам уравнение в своем любимом поисковике. Просто напечатайте что-нибудь вроде y = (x^3 – 7 x + 6)/2, и получится рисунок наподобие тех, которые представлены в этой книге.

В этой главе мы научились легко находить корни любого линейного или квадратного многочлена. А еще есть формулы для нахождения корней многочленов третьей или четвертой степеней, но они очень-очень сложные. Вывели их еще в XVI веке, а потом еще две сотни лет ведущие математики занимались поиском такого же уравнения для многочлена пятой степени. Лучшие умы бились над этой проблемой и никак не могли найти решения, пока в начале XIX века норвежский математик Нильс Абель не доказал, что создать такую формулу для пятой и более высокой степени просто-напросто невозможно. Это приводит нас к каламбуру, который считают забавным только математики: «Почему Исаак Ньютон не смог доказать теорему невозможности формулы для пятого порядка? – Потому что корни с деревьев не падают!»

Примеры доказательств невозможности чего-либо мы рассмотрим в главе 6.

Почему x –1= 1/ x ? Конкретнее, почему 5 –1= 1/5? Взгляните на такую закономерность:

Обратите внимание, что с каждым уменьшением степени на единицу число делится на 5, что имеет для нас смысл, если над этим задуматься. Ведь тогда 5 0= 1, 5 –1= 1/5, 5 –2= 1/25 и так далее. Настоящая же причина этого – правило действий со степенями, согласно которому x a x b= x a+b. Лучше всего он работает, когда a и b – положительные и целые величины. Так, x ² = x · x , а x ³ = x · x · x . Значит,

Если мы хотим, чтобы правило работало при значении степени, равном 0, необходимо, чтобы

а так как левая часть становится равна x a, этому же значению должна быть равна правая часть, что возможно только при x 0= 1.

Желание же применить закон к отрицательным величинам вынуждает нас признать, что

Разделим обе части на x и получим, что x –1должен равняться 1/ x . По той же причине x –2= 1/ x ², x –3= 1/ x ³ и т. д.

Применение закона к целым величинам дает

Следовательно, умножая x ½на x ½, мы получаем x , а это значит, что x ½= √ x (при условии, что x является положительным числом).

Предлагаю закончить главу тем же, с чего мы начинали – с алгебраической магии.

Шаг номер 1. Задумайте два числа от 1 до 10.

Шаг номер 2. Сложите их между собой.

Шаг номер 3. Умножьте сумму на 10.

Шаг номер 4. Прибавьте большее из загаданных чисел.

Шаг номер 5. Теперь вычтите меньшее.

Шаг номер 6. Скажите мне результат, и я назову оба загаданных вами числа.

Хотите – верьте, хотите – нет, но одного этого достаточно, чтобы узнать, с чего все начиналось. Например, если в результате получилось число 126, значит, скорее всего, вы загадали 9 и 3. Даже если повторить этот фокус несколько раз подряд, изумленная аудитория вряд ли догадается, как вы это делаете.