Артур Бенджамин - Магия математики - Как найти x и зачем это нужно

А вот график линий y = 2 x – 2 и y = – x + 7:

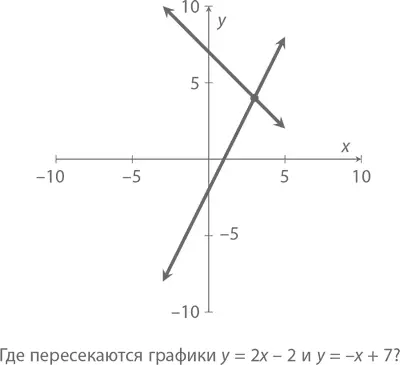
Первая линия y = 2 x – 2 имеет наклон 2 и пересекается с осью Y в точке –2 (график получается параллельным линии y = 2 x + 3 с полным сдвигом вниз по вертикали на 5). Наклон второй линии y = – x + 7 равен –1, поэтому при увеличении x на единицу на ту же единицу уменьшается и y . Призовем на помощь алгебру, чтобы найти точку ( x, y ) пересечения этих двух линий – именно в ней значения наших двух переменных совпадут, и x мы будем искать исходя из того, что он здесь равен y . Иными словами, нам надо решить

Добавим к обеим частям сначала x , потом 2 и получим

то есть x = 3. А зная x , мы можем использовать другое уравнение, чтобы найти y . Если y = 2 x – 2, значит, y = 2(3) – 2 = 4 (а y = – x + 7 дает нам y = –3 + 7 = 4). Значит, графики пересекаются в точке (3, 4).

Зная две точки, лежащие на одной прямой, нарисовать график в виде целой линии становится делом техники. Немного сложнее иметь дело с квадратичной функцией (и фигурирующим в ней x ²). Самое простое для отображения в виде графика – уравнение y = x ² (изображен ниже). Подобные графики называются параболами .

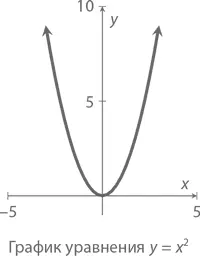
А вот график уравнения y = x ² + 4 x – 12 = ( x + 6)( x – 2).

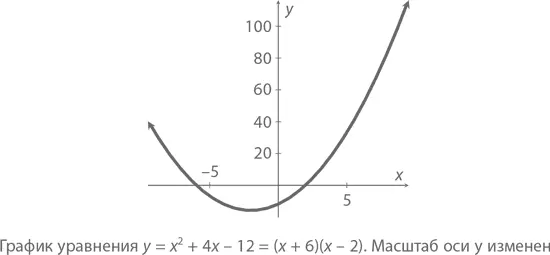
Обратите внимание, что, когда x = –6 или x = 2, y = 0. Это легко заметить на графике – в тех двух его местах, где парабола пересекает ось x . И совсем не случайно, что самая нижняя ее точка располагается точно в центре между ними – при x = –2 и y = –16. Это вершина .

С параболами мы сталкиваемся каждый день. Каждый раз, когда вы видите движущийся по кривой предмет, будь то летящий мяч или струя воды в фонтанчике, вы, в сущности, видите параболу (просто взгляните на картинку чуть ниже). Свойства параболы активно используются в устройстве фар, телескопов, спутниковых тарелок и многих других приборов.

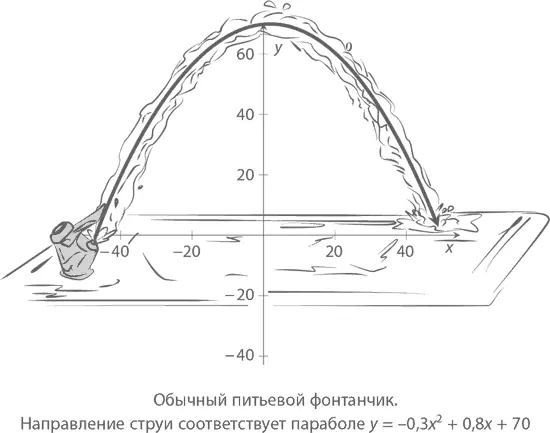
Еще немного терминологии. До этого все наши примеры содержали в себе многочлены – комбинации чисел и одной переменной (скажем, x ), которая может быть возведена в положительную целую степень. Наибольшую из степеней входящего в многочлен одночлена называют степенью многочлена . Например, 3 x + 7 – это (линейный) многочлен первой степени. Многочлен второй степени, вроде x ² + 4 x – 12, называется квадратным , многочлен третьей степени (5 x ³ – 4 x ³ – √2) – кубическим . Бывают многочлены и других, бóльших, степеней (я, правда, никогда не слышал их специальных названий – главным образом, думаю, потому, что не так уж и часто они встречаются. Интересно, насколько часто используются в профессиональной литературе термины «квартический», «квинтический» и т. п. многочлены? Встречаются, наверное, но я, честно говоря, по этому поводу настроен немного скептически). А еще бывают многочлены, в которых нет переменных (например, 17) – о таких говорят, что они стоят в нулевой степени . Ну и последнее, что вам нужно знать о многочленах – это то, что многочленом не может быть сочетание с бесконечным количеством чисел. Например, 1 + x + x ² + x ³ +… – не многочлен, а так называемый бесконечный ряд , о которых мы поговорим подробнее в главе 12.

Обратите внимание, что в случае с многочленами степень, в которую возводятся переменные, может быть выражена только положительным целым числом – ни в коем случае не отрицательным и не дробным. То есть если вам попадается уравнение с чем-нибудь вроде y = 1/ x или y = √ х , это не многочлен, потому что 1/ x = x –1, а √ х = x ½.

Корнями многочлена мы считаем такие значения х , при которых многочлен равняется 0. Например, 3 x + 7 имеет один корень, а именно x = –7/3. А вот у x ² + 4 x – 12 два корня: x = 2 и x = –6. А x ² + 9 корня (в смысле, действительного корня) не имеет вообще. Обратите внимание, что каждый многочлен степени 1 ( линейный ) имеет один корень в силу того, что он пересекает ось X только в одной точке, квадратный – не больше двух. Многочлены x ² + 1, x ² и x ² – 1 имеют соответственно ноль, один и два корня.