Сложность постановки:средняя (требуется массовка).
Использование:чтение, театр, съемка.
Школьный класс, урок математики. Рядом с У. сидит В.
У:Сегодня у нас проверяющий из РОНО Василий Сергеевич, кандидат математических наук. Покажем ему, чего мы достигли. Маша, расскажи нам о теореме Пифагора.
М: (выходит к доске, пишет). a 2+b 2=c 2. В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
В:Правильно. Но я вижу, не все в вашем классе внимательно слушают урок (показывает на Г. на последней парте).
У:Это Глеб, двоечник, весь урок отвлекается, играет на планшете…
В:Глеб, что ты можешь добавить к ответу Маши?
Г: (с удивлением отрывается от планшета). Неправильно она ответила. Не сумма, а разность.
У:Да что ты говоришь! Может, докажешь?
Г: (нехотя выходит к доске, пишет, см. рис. 1) . Да легко. Берем бесконечно малые приращения катетов a, b и гипотенузы с, сохраняющие подобие с исходным прямоугольником и получаем такие дифференциальные соотношения:
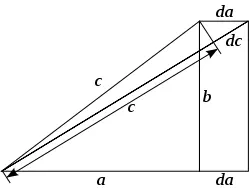
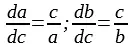 [1]
[1]
Откуда 
Применяя формулу разделения переменных, получаем диффур:
сdc = ada – bdb [3]
Интегрируем:
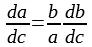 или
или
c 2=a 2—b 2[6]
В: (обалдело смотрит на доску). Это неверная формула! Сейчас я найду ошибку…
Г:Ищите. Я пока поиграю (уходит к своей парте) .

Смена картинки. Звенит звонок, никто не обращает на него внимания. Все смотрят на В., покрывшего соседнюю доску мелкими формулами (рис. 2). В класс входит Т.
Т:Звонок давно, последний урок. Что не выходите?
В: (с взъерошенными волосами и безумными глазами). Не мешайте, мы здесь решаем мировую проблему математики! Неужели Пифагор ошибался?!
Т: (быстро просматривает «доказательство» Г.). В дифференциальном уравнении неправильно разделены переменные. Будет плюс, а не минус (исправляет минус на плюс в 3-й формуле) . Давайте выметайтесь все. Мне убираться надо.
Практическое доказательство
Действующие лица: Глеб (Г), Саша (С).
Место действия: квартира.
Реквизит: линейка, мухобойка, ножницы.
Возраст: 11–14 лет.
Сложность постановки:легкая.
Использование:чтение, театр, съемка.
Лето, квартира, С. и Г. сидят за столом.
С:Меня прикрепили к тебе подтянуть геометрию и я это сделаю. Времени у нас много – все летние каникулы. Начнем с азов. Любые три точки всегда лежат в одной плоскости.
Г:Доказательство?
С:Нет. Это аксиома.
Г: (водит руками в воздухе). Что-то мне не верится (осматривается, берет мухобойку). Смотри, ведь плоскость? А мухи ведь как точки? Давай проверим твое утверждение (передает мухобойку С.)
С. бьет мухобойкой.
Г: (осматривает мухобойку). Две мухи. Не подтверждено.
С. бьет мухобойкой.
Г: (осматривает мухобойку). Вообще одна.
С. бьет мухобойкой.
Г: (осматривает мухобойку). Три. Но это может быть случайность. Нужно набрать статистику.
Смена картинки. Утомленный С. полулежит на диване.
С:Ох, утомился я с этой проверкой!
Г: (подходит к С. с ножницами и линейкой). Теперь осталось доказать, что пифагоровы штаны во все стороны равны. Ты не Пифагор, но штаны снимай – отрежем как надо и измерять будем!
С. обалдело смотрит на Г.
Действующие лица: Глеб (Г), учитель (У).
Место действия: школьный урок.
Реквизит:
Возраст: 9–14 лет.
Сложность постановки:легкая.
Использование:чтение, театр.
На доске надпись: «Основы математической логики». Г. шепчется с соседом по парте.
У:Глеб, ты хочешь отвечать?
Г:Нет, вы же сказали, что хотите неожиданно меня вызовите в этой четверти. А это невозможно.
Читать дальше
Конец ознакомительного отрывка
Купить книгу


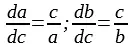 [1]
[1]
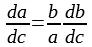 или
или











