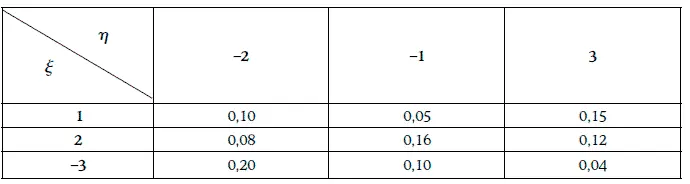
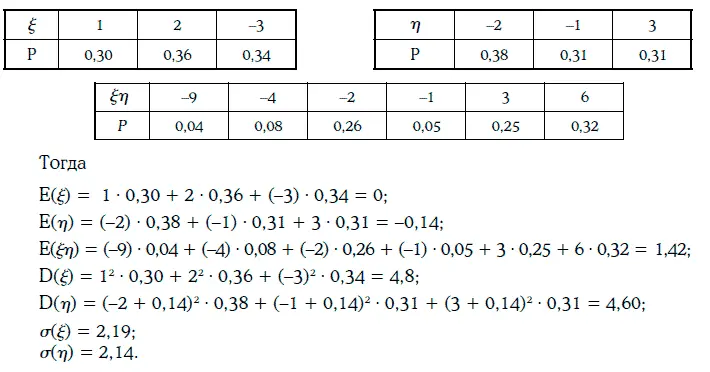
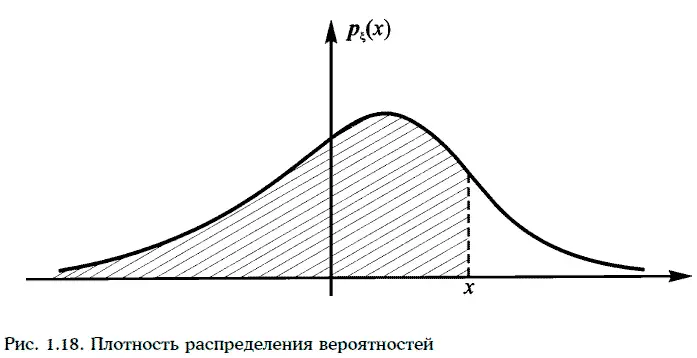
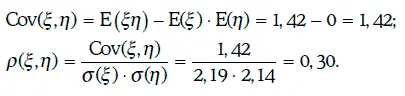Алексей Лобанов - Энциклопедия финансового риск-менеджмента
Здесь есть возможность читать онлайн «Алексей Лобанов - Энциклопедия финансового риск-менеджмента» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Город: Москва, Год выпуска: 2019, ISBN: 2019, Жанр: management, management, popular_business, на русском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Энциклопедия финансового риск-менеджмента
- Автор:
- Жанр:
- Год:2019
- Город:Москва
- ISBN:978-5-9614-2284-9
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Энциклопедия финансового риск-менеджмента: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Энциклопедия финансового риск-менеджмента»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Книга предназначена для профессионалов, непосредственно занимающихся оценкой и управлением рисками, преподавателей, студентов и аспирантов экономических факультетов вузов. Она также может использоваться для подготовки к сдаче международных экзаменов по финансовому риск-менеджменту на получение сертификатов Financial Risk Manager (FRM®) и Professional Risk Manager (PRM®).