Майкл Рейнор - Как думают великие компании - три правила

Чтобы вам было легче понять наш подход к этой проблеме, ниже мы приводим в сокращенном виде таблицу 6 из главы 3, в которой оценивается вероятность связи между относительной конкурентной позицией и относительной рентабельностью в наших выборках с использованием попарных сравнений (в таблице 6 мы рассматриваем наши тройки как целое, и поэтому в каждой из них одна компания занимает «промежуточную» конкурентную позицию; при попарных сравнениях можно сравнивать только ценовые и неценовые позиции).

При сравнении «чудотворцев» с «середнячками» легко видеть, что семь «чудотворцев» имеют неценовую конкурентную позицию, и два имеют ценовую позицию. В каждом случае между «чудотворцами» и «середнячками» имеются определенные различия.

Эта выборка из 9 попарных сравнений составляет 5,2 % от нашей группы из 174 «чудотворцев», и возможные ложноотрицательные результаты здесь не учитываются. Если бы наша выборка была абсолютно репрезентативной по отношению к нашей группе в целом, мы могли бы с полным основанием сделать вывод, что «чудотворцы» имеют неценовые конкурентные позиции относительно «середнячков» в течение 78 % рассматриваемого времени, то есть в подавляющем большинстве случаев, и это убедительно доказывало бы наличие сильной связи между выдающейся рентабельностью и неценовыми конкурентными позициями.

Таблица 51 . Относительные конкурентные позиции при попарном сравнении

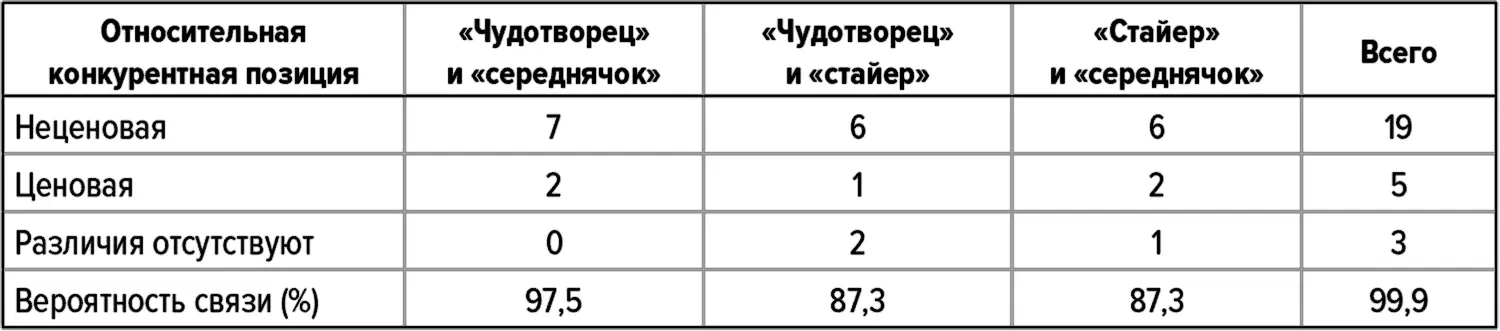
Источник: анализ, выполненный авторами.

При ссылках на нашу «группу» из «чудотворцев» и «стайеров» мы игнорируем проблему возможных ложноотрицательных результатов.

Однако наша выборка, скорее всего, не вполне репрезентативна, прежде всего – из-за ее небольшого размера. Получить экстремальный результат в небольшой выборке гораздо легче, чем в большой. В обычном случае можно было бы рассчитать доверительный интервал для нашей оценки 78 %, но для малых выборок этот метод непригоден. Вместо этого мы намереваемся проверить вероятность того, что наша выборка могла быть получена из распределения, в котором равновероятными являются три возможных результата. Так, если мы предположим, что компания-«чудотворец» с одинаковой вероятностью может иметь неценовую, ценовую и такую же относительную конкурентную позицию, как и «середнячок», мы сможем оценить вероятность получения выборки, которую мы фактически получили.

Если использовать аналогию, это можно уподобить оценке вероятности того, что монета действительно симметрична, по результатам определенного числа бросков. Если предполагается, что монета симметрична, и если из 10 бросаний выпадает 6 орлов, то вероятность несимметричности монеты с повышением частоты выпадения орлов равна вероятности выпадения 6 и более орлов из 10 бросаний, то есть 38 %. На этом этапе оценка становится субъективной. Означает ли это, что вероятность того, что монета симметрична, составляет только 38 % ? Или это означает, что монета, вероятно, симметрична? Если бы это было возможно, вы собрали бы больше данных. Если вы не можете собрать больше данных, необходимо сделать вывод на основании имеющихся данных или вообще воздержаться от выводов.

При тестировании моделей со множеством ячеек, как в приведенной выше таблице, обычно ищут значимую кластеризацию в таблицах сопряженности признаков с помощью так называемой статистики хи-квадрат. Однако для малых выборок (например, когда N < 30) и для случаев, когда ожидаемое число ячеек меньше 5 более чем для 20 % ячеек, этот метод непригоден. Например, если у нас 9 компаний в столбце или строке, то следует ожидать, что число компаний в каждой ячейке будет равно 9/3, что меньше 5.

С учетом этого мы продолжим аналогию с моделированием. Предположим, что мы бросаем гипотетическую «симметричную» трехстороннюю монету k раз, где k – число компаний в строке или столбце. Затем мы оцениваем вероятность попадания m или более смоделированных компаний в одну и ту же ячейку. Мы повторяем этот процесс 10 миллионов раз, вычисляя процент времени, в течение которого m или более моделируемых компаний из k попадают в одну ячейку.

Таким образом, на самом деле мы проверяем, можно ли ожидать, что не меньше чем m компаний из k могут собраться вместе в любой из трех ячеек в строке (или столбце) случайным образом. Итак, приведенные выше значения в % – это вероятности того, что наблюдаемая кластеризация не является случайной («случайной» означает, что все фирмы имеют одинаковую вероятность [p = ⅓] попадания в каждую ячейку). Однако мы не утверждаем, что вся группа выглядит как наша выборка. Скорее мы утверждаем, что судя по нашей выборке, чтобы сделать выгодное вложение, нужно учитывать наличие систематических связей между относительной конкурентной позицией и результатами попарных сравнений.