Елена Жидкова - Развитие учетно-аналитической концепции контроллинга. Теория и методология

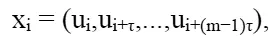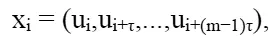
где m – размерность вложения и τ – запаздывание по времени (реальное запаздывание по времени определяется как τΔt). Данная операция называется «погружением аттрактора» в пространство размерности m. Результатом успешного погружения является выявление определенных закономерностей в поведении траектории системы в пространстве данной размерности. Сохранение топологических структур исходной траектории гарантировано, если m ≥ 2d + 1, где d – размерность аттрактора.

Отметим несколько важных следствий, вытекающих из теоремы Такенса:

1) в непрерывной системе, состояние которой измеряется временным шагом (t), один и тот же результат получается почти для всех т;

2) один и тот же результат будет получен при измерении практически любой величины компоненты временного ряда;

3) если имеет место распределенная система, в которой есть диссипативные процессы, то неважно в какой точке пространства проводить измерения.

Теорема Такенса предполагает, что закон развития ряда не меняется во времени. Как правило, наблюдаемые временные ряды (в частности, финансовые, инвестиции) для предсказания тенденций в экономических системах отличаются сильной нестационарностью. Таким образом, данное предположение в подавляющем большинстве случаев является неоправданным. На практике предсказательная сила метода оказывается весьма низкой.

Ввиду того что наблюдаемая информация об исходной системе недостаточна, следует учитывать как динамические, так и статистические характеристики временного ряда. Таким образом, при построении модельной системы можно совместно использовать динамические и вероятностные компоненты, то есть задействовать метод русел и джокеров.

Использование идеи русел позволяет делать прогнозы для систем большой размерности, которые оказываются вне пределов применимости малодомовой нелинейной динамики (термин «малодомовой» показывает, что алгоритмы теряют эффективность для систем с размерностью аттрактора d > 5, т. е. с числом наиболее существенных переменных 5 × 10). К примеру, в некоторой области G (рис. 18) различные траектории могут оказаться близкими в проекции. Тогда в этой проекции динамика становится частично предсказуемой, и такая «модель» в проекции будет иметь принципиально ограниченную точность. В данной ситуации усредненная модель представляет собой «проекцию» на пространство медленно меняющихся мод, но в отличие от них, здесь модель справедлива только при попадании траектории в область G. Как только траектория исходной системы покинет эту область, предсказуемость в проекции будет утрачена [113]. При нахождении в области русла система ведет себя предсказуемо и дает возможность получать достаточно точный прогноз ее динамики на некоторый период.

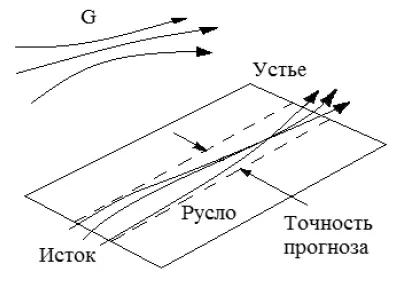
Рис. 18. Схема возникновения русла [113, с. 303]

Наиболее адекватной моделью для русла следует признать динамическую систему с наложенным шумом. Вероятно, этот «шум» должен обладать некоторыми динамическими чертами, чтобы воспроизводить свойства проекции траектории в пространстве большой размерности [113]. В случае прохода траектории системы по руслу достаточное число раз по временному ряду с определенной степенью достоверности можно определить проекцию системы и предсказать ее поведение.

Когда русло кончается, начинает быстро расти число переменных, определяющих ход процесса, при этом уменьшается горизонт прогноза и появляется возможность резких изменений. Области устойчивого движения в фазовом пространстве могут сменяться областями неустойчивого, плохо предсказуемого, зашумленного или даже случайного движения.

В соответствии с концепцией русел и джокера в фазовом пространстве многих реальных объектов имеются области джокеров, в которых случайность или фактор не только оказывают решающее влияние на дальнейшую судьбу системы, но и могут скачком перевести ее в другую точку фазового пространства. Функция джокера в данном случае состоит в мгновенном перемещении системы из одного русла в другое.

На рисунке 19 приведены два русла (G 1и G 2) и 3 джокера (J 1, J 2, J 3). Черные стрелки показывают детерминированное описание динамики (траектории модели для проекции), «пустые» стрелки показывают действия джокеров: когда траектория попадает в область джокера (заштрихованную), она может с некоторой вероятностью направиться в какую-то случайную точку русла или к другому джокеру [113]. Соответственно, в области джокера достоверный прогноз сделать практически невозможно.