Елена Жидкова - Развитие учетно-аналитической концепции контроллинга. Теория и методология

Появление джокеров в фазовом пространстве динамической системы определяется следующими признаками:

– локальная неустойчивость системы с хаотическим поведением, чередуясь с устойчивым движением, формирует странные аттракторы;

– сильная перемежаемость (когда происходит смена режимов поведения с относительно высокой скоростью);

– влияние внешних шумов в локальных областях;

– высокомодовое движение системы;

– наличие разрывов в отображении;

– быстрые системные изменения, происходящие в объекте, в том числе и критические [230].

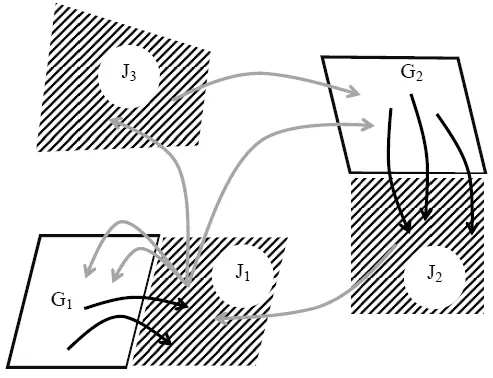
Рис. 19. Схема представления сложной динамики как комбинации русел и джокеров [113, с. 305]

Однако все эти признаки, кроме разрывов в отображении, можно обнаружить только в случае, если возможно использование метода активного пространств возрастающей размерности по данным временного ряда.

Исходя из специфики рассматриваемой задачи, предусматривается использование следующих видов джокеров:

– дискретный точечный джокер, который мгновенно приводит систему в определённую точку фазового пространства. Как правило, это связывается с ситуацией, когда хаос в системе обязательно повлечет за собой ее разрушение;

– двухточечный джокер, который при срабатывании с вероятностью p 1и вероятностью р 2переводит систему в ту или иную точку фазового пространства;

– непрерывный джокер переводит систему в точку некоторой области фазового пространства в соответствии с заданным законом распределения вероятности. Данный тип джокера следует рассматривать как обобщение точечного и двухточечного джокеров;

– мерцающий непрерывный джокер выражается, по сути, непрерывным джокером. Срабатывает он с некоторой, отличной от 1, вероятностью, то есть при попадании изображающей точки в область джокера следующий шаг либо (с вероятностью р 1 и делается в соответствии с уравнением русла, либо (с вероятностью р 2) в соответствии с правилом непрерывного джокера. Этот тип джокеров хорошо подходит для имитации явления перемежаемости;

– мерцающий точечный джокер представляет собой точечный джокер, который срабатывает аналогично мерцающему непрерывному джокеру, в соответствии с вероятностным правилом [26; 112].

Следует отметить, что с позиций динамической теории информации, особого внимания заслуживает промежуток времени непосредственно перед выходом системы из перемешивающего слоя, так как после выхода дальнейшее поведение системы полностью предсказуемо, а сразу после входа – полностью непредсказуемо. Следовательно, отрезок времени перед выходом системы требует формирования качественного интеллектуального продукта для принятия решений.

Процесс бизнес-анализа сочетается с прогнозированием хода различных процессов, скоординированное выполнение которых предполагает достижение бизнес-цели.

Макросистема, оказывающая координирующее и управляющее воздействие на систему нижележащего уровня, позволяющая задать общие пределы движения в терминах смены русел и джокеров, будет находиться в принципиально ином временном масштабе. Пока макросистема находится в русле, задаваемые ею параметры порядка, управляющие состоянием микросистемы, стабильны. Даже если микросистема (отдельный экономический субъект) идентифицирует приближение области джокера, выход из джокера, выбор новой траектории из точки бифуркации, фактически предопределен тем коридором возможностей, который обеспечивает стабильное русло макросистемы, а это означает возможность вероятностного прогнозирования риска для разных сценариев выхода из джокера. Интересы макро– и микроуровней экономической системы имеют различия как в руслах, так и в джокерах.

Одной из задач бизнес-анализа в системе контроллинга наряду с прогнозированием деятельности является ранняя диагностика дестабилизации состояния системы на сигнально-информационной основе с целью избежать попадания в область джокера, а в случае нахождения в ней своевременно отреагировать на кризисную ситуацию. Каждое экономическое событие должно происходить в неком пространстве. Следовательно, в построении модели должно быть определено пространство, на котором задана система, и очень точно оговорены допущения, исходные данные.

При изучении свойств сложных систем в экспериментальных исследованиях широко используется подход, основывающийся на анализе сигналов, произведенных системой. Сигнал представляется временным рядом значений, наблюдаемых в последовательные моменты времени: x(t)≡{x 1, x 2,…,x N }, где t≡{t 1,t 2,…,t N}, x i=x(t i), i =1…N, где N – число отсчетов в сигнале. Сложные сигналы, которые снимаются с большинства реальных систем, обладают следующими характеристиками (одной или несколькими): нестационарны, нерегулярны, функция распределения сигнала отлична от нормального, сингулярны, фрактальны, стохастичны и хаотичны. Решение задач прогнозирования таких сигналов невозможно без реализации в программных комплексах.