А. Красько - Схемотехника аналоговых электронных устройств

В подразделе 2.3 приведена основная идея обобщенного метода узловых потенциалов, на основе которого были получены большинство соотношений для эскизного расчета усилительных каскадов. Однако наряду с несомненными достоинствами данного метода (простота программирования, малая размерность получаемой матрицы проводимости Y, n*n, где n- количество узлов схемы без опорного), данный метод имеет ряд существенных недостатков. В первую очередь следует отметить невозможность представления в виде проводимости некоторых идеальных моделей электронных схем (короткозамкнутых ветвей, источников напряжения, зависимых источников, управляемых током и т.д.). Кроме того, представление индуктивности проводимостью неудобно при временном анализе схем, что связано с преобразованием Лапласа (оператор Лапласа pдолжен быть в числителе для того, чтобы система алгебраических уравнений и полученная в результате преобразования система дифференциальных уравнений имела одинаковые коэффициенты).

В настоящее время наибольшее распространение получили топологические методы формирования системы уравнений электрической цепи, наиболее общим из которых является табличный [4].

В этом методе все уравнения, описывающие цепь, включаются в общую систему уравнений, содержащую уравнения Кирхгофа для токов, напряжений и компонентные уравнения.

Уравнения Кирхгофа для токов можно представить в виде

AI в = 0,

где A — матрица инценденции [4], описывающая топологию цепи, I в — вектор тока ветвей.

Уравнения Кирхгофа для напряжений имеют вид

V в – A tV п = 0,

где V в и V п — соответственно, вектора напряжений ветвей и узловых потенциалов, A t — транспонированная матрица инценденции A.

В общем случае уравнения, описывающие элементы цепи, можно представить в следующей форме:

Y вB в + Z вI в = W в ,

где Y в и Z в — соответственно, квазидиагональные матрицы проводимости и сопротивления ветвей, W в — вектор, куда входят независимые источники напряжения и тока, а также начальные напряжения и токи на конденсаторах и индуктивностях.

Запишем приведенные уравнения в следующей последовательности:

V в – A tV п = 0;

Y вB в + Z вI в = W в ;

AI в = 0;

и представим в матричной форме

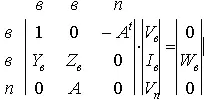
или в общем виде

TX=W.

Табличный метод имеет главным образом теоретическое значение, поскольку наряду с основным достоинством, выражающимся в том, что возможно нахождение всех токов и напряжений ветвей и узловых потенциалов, имеет ряд существенных недостатков. В первую очередь следует отметить избыточность метода, приводящую к большой размерности матрицы T. Далее следует отметить, что многие идеальные управляемые источники приводят к появлению лишних переменных. Например, входной ток управляемых напряжением источников тока и напряжения, а также входное напряжение управляемых током источников тока и напряжения равны нулю, но в данном методе они рассматриваются как переменные.

В практическом плане чаще всего используется модификация табличного метода — модифицированный узловой метод с проверкой [4].

Идея данного метода заключается в разделении элементов на группы; одна группа сформирована из элементов, которые описываются помощью проводимостей, для элементов второй группы такое описание невозможно. Поскольку через токи ветвей первой группы можно выразить напряжения ветвей, а напряжения ветвей через узловые потенциалы, то можно исключить из табличных уравнений все напряжения ветвей, а для элементов первой группы еще и токи ветвей. При введении дополнительных уравнений для токов в ветвях с элементами второй группы производится проверка на наличие заранее известных (нулевых) переменных. В результате такого преобразования получим уравнения модифицированного узлового метода с проверкой

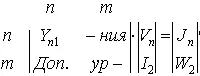
или в общем виде

T mX=W,

где n — размерность матрицы проводимости Y n 1 элементов первой группы (n — число узлов схемы без нулевого); m — число дополнительных уравнений для элементов второй группы; J n — вектор независимых источников тока; I 2 — вектор токов ветвей элементов второй группы; W 2 — вектор, куда входят независимые источники напряжения, а также начальные напряжения и токи на конденсаторах и индуктивностях, представленных элементами второй группы.