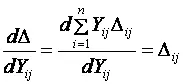А. Красько - Схемотехника аналоговых электронных устройств

Для определения производных алгебраических дополнений по изменяемым параметрам входящих в них элементов воспользуемся теоремой, утверждающей, что производная определителя по какому-либо элементу равна алгебраическому дополнению этого элемента. Доказательство теоремы основано на разложении определителя по Лапласу

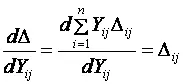
Общее выражение для S-параметров через алгебраические дополнения имеет вид (см. подраздел 7.2)

S ij = k ij Δ ji /Δ – δ ij .

Определим функции чувствительности параметров рассеяния к пассивному двухполюснику y o включенному между произвольными узлами k и l (см. рисунок 8.5а)

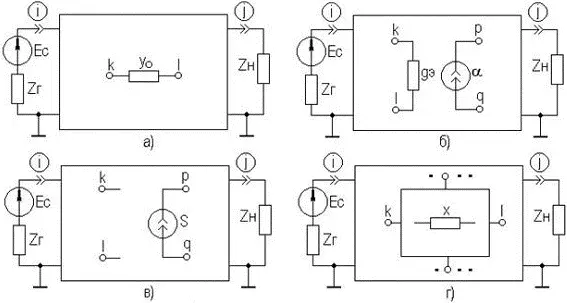
Рисунок 8.5. Расчёт чувствительности S-параметров

S S ij y 0= dS ij / dy 0= k ij (Δ ji ( k + l )( k + l )Δ – Δ ( k + l )( k + l )Δ ji )/Δ² = – k ij Δ j ( k + l )Δ ( k + l ) i /Δ² = – k ij [(Δ jk – Δ jl )(Δ ki – Δ li )]/Δ²

При получении данного и последующих выражений используются следующие матричные соотношения [3]:

Δ ( i+j )( k+l )= Δ i ( k+l )+ Δ j ( k+l )= (Δ ik – Δ il ) + (Δ jk – Δ jl ),

Δ ij Δ kl – Δ il Δ kl = ΔΔ ij,kl .

Для электронных схем, содержащих БТ, моделируемые ИТУТ (см. подраздел 2.4.1), определим чувствительность S-параметров к проводимости управляющей ветви g э =1/ r э и параметру управляемого источника a включенных соответственно между узлами k, l, и p, q (рисунок 8.5б):

S S ij gэ = dS ij / dg э = k ij [(Δ ji ( k + l )( k + l )Δ + αΔ ij ( k + l )( p + q ))Δ – (Δ ( k + l )( k + l )Δ+αΔ ( k + l )( p + q )Δ ij ])/Δ² = – k ij Δ ( k + l ) i (Δ j ( k + l )+ αΔ j ( p + q ))/Δ² = – k ij (Δ ki– Δ li )[(Δ jk– Δ jl )+ α(Δ jp - Δ jq )/Δ²,

S S ij α= dS ij / d α = k ij (Δ ji ( k + l )( p + q )Δ – Δ ( k + l )( p + q )Δ ji )/Δ² = – k ij Δ j ( p + q )Δ ( k + l ) i /Δ² = – k ij [(Δ jp– Δ jq )(Δ ki– Δ li )]/Δ².

Если электронная схема содержит ПТ, моделируемые ИТУН (см. подраздел 2.4.1), то чувствительность параметров рассеяния к крутизне S, включенной между узлами p, q при узлах управления k, l (рисунок 8.5в), равна

S S ij S= dS ij /dS = k ij (Δ ji ( k + l )( p + q )Δ – Δ ( k + l )( p + q )Δ ji )/Δ² = – k ij Δ j ( k + l )Δ ( p + q ) i /Δ² = – k ij [(Δ jk– Δ jl )(Δ pi– Δ qi )]/Δ².

Чувствительность параметров рассеяния к любому Y-параметру подсхемы (рисунок 8.5г), например, y kl , будет равна

S S ij ykl = dS ij / dy kl = k ij (Δ ji,kl Δ – Δ kl Δ ij )/Δ² = – k ij Δ jl Δ ki /Δ².

При известной чувствительности y kl к параметру элемента подсхемы x (см. рисунок 8.5г) чувствительность S-параметров полной схемы к этому параметру, в соответствии с понятием сложной производной, выразится как

S S ij x= ( dS ij / dy kl )( dy kl / dx ) = S S ij ykl · S y kl x .

Последнее выражение указывает на возможность применения метода подсхем при анализе чувствительности сложных электронных схем.

Зная связь параметров рассеяния с вторичными параметрами электронных схем ( K U , Z вх , Z вых и др.) и чувствительность параметров рассеяния к изменению элементов схемы, возможно нахождение функций чувствительности вторичных параметров к изменению этих элементов. Например, для коэффициента передачи по напряжению с i-го на j-й узел K ij = S ji /(1+ S 11) чувствительность к изменению параметра x (полагая, что S ij = f ( x ) и S ii =φ( x )) получаем

S K ij x = dK ij / dx = [ S S ij x (1 + S ii ) – S S ii xS ij ]/(1 + S ii )².

Аналогично для Z вх ( вых ) ( Z ii ( jj )) имеем

Z ii ( jj ) = Z г ( н )·(1 + S ii ( jj ))/(1 – S ii ( jj ));

S Z i i ( jj ) x = dZ ii ( jj )/ dx = –2 Z г ( н )· S S i i ( jj ) x ·S ii ( jj )/(1 – S ii ( jj ))².

Данный способ столь же эффективно может быть использован при определении чувствительности более высоких порядков для всевозможных характеристик электронных схем. Реализация полученных таким образом алгоритмов расчета чувствительности сводится к вычислению и перебору соответствующих алгебраических дополнений, что хорошо сочетается с нахождением других малосигнальных характеристик электронных схем.