Петр Путенихин - Правила счета элементов бесконечного множества

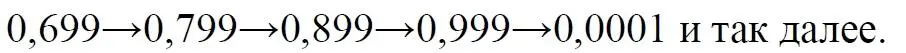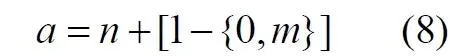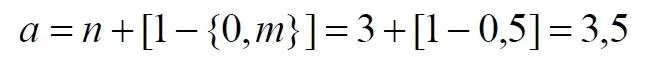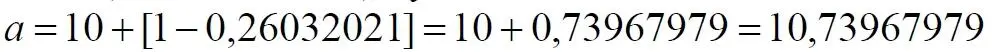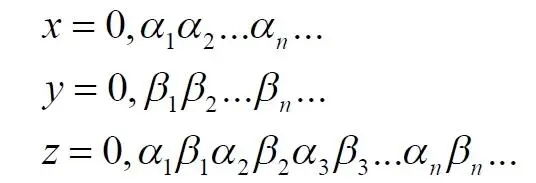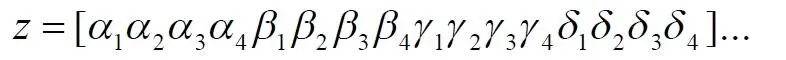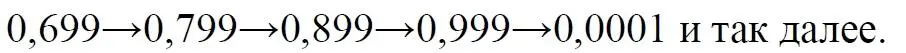
Последовательность чисел в таблице будет содержать все без исключения числа. Собственно правило формирования чисел имеет простое аналитическое выражение, подобное (3) или (6). Возьмем два натуральных числа m и n, изменяющиеся от 0 до бесконечности. Запишем с их помощью некоторое число в виде

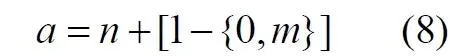
Здесь запись {0,m} означает число, меньшее единицы, дробной частью которого является натуральное число m. Фактически при табличной записи чисел n является номером строки в таблице, а m – номером колонки. Например, в ячейке (n=3; m=5) будет находиться число:

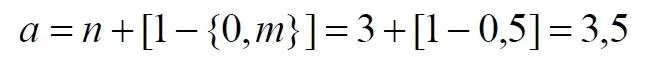
а в ячейке (n=10; m=2021) будет находиться число

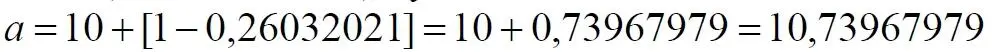
Для составления таблицы начнем перебирать, подсчитывать все получившиеся числа. Строки чисел будут иметь вид:

Знаки плюс в таблице означают не суммирование, а используются как разделитель между числами. В связи с повторами, поскольку числа вида 0,1+0,10+0,100+0,1000 в использованном алгоритме считаются разными, общее количество чисел, видимо, окажется больше примерно на 10%. Конечно, мы можем повторяющиеся числа пропускать, не считать, но 10% погоды не делают. Если изобразить расположение чисел на графике, то график будет иметь вид пилы.

Для большей общности можно добавить еще одно условие: четные числа n будем делить на 2 и полученное число записывать согласно выбранному виду. Для следующего нечетного числа n запишем то же самое число, только со знаком минус. Очевидно, что в такой ряд легко включить и все вещественные и действительные, комплексные числа и даже кватернионы. Нумерация сформированных чисел соответствует нумерации членов любого числового ряда, то есть, каждое число из таблицы получит свой индивидуальный натуральный порядковый номер , будет пронумеровано при подсчёте. Каким бы ни было количество всех действительных чисел, наше движение по ряду не пропустит ни одного из них, и каждое из них получит свой индивидуальный натуральный номер. Таким образом, можно сделать вывод: континуум является счетным. Используя обратный метод индексации Кантора [3, с.77], мы можем корректно включить в этот континуум все мыслимые виды чисел. Как известно, метод Кантора формирует новое число из двух следующим образом:

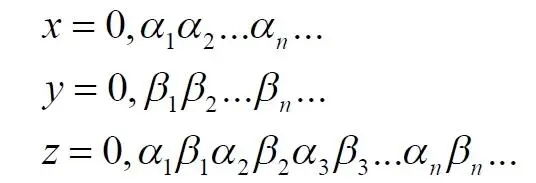
У двух рациональных чисел x и y берутся цифры после запятой и поочередно вписываются после запятой третьего числа z. Мы проделаем обратную операцию, сформируем из одного числа несколько коэффициентов, например, для кватерниона. Возьмем из полученного ряда какое-либо число z и будем рассматривать его как составное, отбросив ноль и запятую:

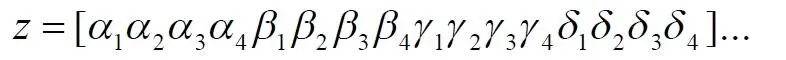
Очевидно, что все составляющие число цифры гарантируют любую комбинацию, поскольку ряд чисел z бесконечен. Теперь составим из одноименных цифр новое число, кватернион:

Здесь в каждом коэффициенте показаны только четыре цифры, но, очевидно, их может быть любое количество. Также очевидно, что и самих коэффициентов может быть любое число: один коэффициент даёт действительное или вещественное число, два коэффициента дают комплексное число и так далее.

Понятно, что полученный ряд всех возможных чисел является счетным, каждое из исходных чисел имеет свой индивидуальный натуральный порядковый номер. Среди этих чисел обязательно окажутся и число е (2,71828…), и π (3,14159…), и константа пропорциональности С (0,76422…) Ландау – Рамануджана, и постоянная тонкой структуры . Счетность ряда обеспечивается использованием метода квадратов, предложенного математиком-филателистом из рассказа об отелях с бесконечным числом номеров [3, с.57] являющегося эквивалентом диагонального процесса Кантора: