Жан-Поль Эймишен - Электроника?.. Нет ничего проще!

Н. — Я уже объяснил тебе: она шунтирует резистор и на высоких частотах снижает значение результирующего сопротивления.

Л. — Я хотел бы внести некоторые уточнения. Предположим, что емкость С равна 16 пф (чтобы упростить расчеты ее реактивного сопротивления), тогда ее сопротивление равно 1 Мом на 10 кгц, 100 ком на 100 кгц, 10 ком на 1 Мгц и 1 ком на 10 Мгц. Предположим, что сопротивление резистора R 2 = 100 ком. Скажи, пожалуйста, на какой частоте начнет тебе мешать емкость С ?

Н. — Для этого следовало бы рассчитать результирующее (полное) сопротивление включенных параллельно резистора R 2 и конденсатора С . Но я могу тебе сказать, что на частоте 10 кгц влияние емкости С с ее реактивным сопротивлением 1 Мом на входное сопротивление устройства, близкое к 100 ком, будет очень мало.

Л. — Я бы даже сказал, что ее воздействие на полное сопротивление практически равно нулю (не больше 0,5 %). Но посмотри, Незнайкин, проходящий по емкости С ток на 90° опережает ток, проходящий по R 2 . Я обозначил эти токи стрелками (рис. 38), а вернее векторами, характеризующими их амплитуду и фазу. Для определения полного тока построим прямоугольник, сторонами которого являются две названные стрелки. Диагональ прямоугольника соответствует стрелке, характеризующей полный ток. Но на частоте 10 кгц максимальный ток I с , проходящий через конденсатор, в 10 раз меньше тока, проходящего через резистор. Диагональ прямоугольника при этом настолько близка к его большей стороне, что их можно спутать. Если ты слышал о теореме Пифагора…

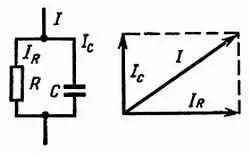
Рис. 38. К Rи Сприложено одно и то же напряжение, протекающий через конденсатор Сток I сна 90° опережает I R(ток, протекающий через резистор). Полный ток Iпредставляет собой векторную сумму токов I си I R.

Н. — Хм, очень немного и, по правде сказать, плохо понял.

Л. — Эта теорема гласит, что диагональ прямоугольника (или гипотенуза прямоугольного треугольника, который представляет собой половину прямоугольника) равна корню квадратному из суммы квадратов его сторон. В нашем случае одна сторона равна 10, а другая — 1, следовательно, сумма квадратов составит 101, а корень квадратный — 10,05.

Н. — Очень любопытно, в самом деле, наличие паразитной емкости на частоте 10 кгц никак не сказывается на коэффициенте усиления.

Л. — Емкость С в этом случае не оказывает заметного влияния на коэффициент усиления, но влияет на вносимый усилителем сдвиг фазы. Посмотри: общий ток (диагональ) находится в фазе с приложенным к сетке напряжением U c= U вх, тогда как напряжение на выходе, естественно, находится в фазе с током, проходящим по резистору R 2 (большая сторона). Как ты видишь, между ними уже имеется сдвиг по фазе, пренебрегать которым нельзя (здесь около 6°). Когда же реактивное сопротивление емкости С будет всего лишь в 3 раза больше сопротивления R 2 (т. е. на частоте 33 кгц), образованный стрелками прямоугольник все еще будет довольно вытянутым и его диагональ всего лишь на 5 % длиннее большой стороны. Иначе говоря, проходящий по резистору ток будет составлять 95 % общего тока, коэффициент усиления еще составит 95 % коэффициента усиления на низкой частоте. Но сдвиг фазы станет очень значительным (больше 18°).

Н. — Если ты будешь так продолжать, то дойдешь до того, что скажешь мне, что влияние С на коэффициент усиления так никогда и не почувствуется!

Л. — Вовсе нет. Когда реактивное сопротивление С достигнет величины R 2 , т. е. 100 ком, прямоугольник, о котором я говорил, станет квадратом. Сторона квадрата равна всего лишь 0,7 его диагонали (1:√2), коэффициент усиления в этом случае снизится до 0,7 своего значения на низких частотах, сдвиг фазы увеличится до 45°, т. е. мы достигли так называемой «граничной» частоты, на которой коэффициент усиления снижается на 30 % от своего максимального значения. Говорят, что он снизился на 3 дб и…

Н. — С децибелами я немного не в ладах.

Л. — И вместе с тем это очень просто. Белы (обычно пользуются десятыми долями этой величины) выражаются десятичным логарифмом отношения мощностей.