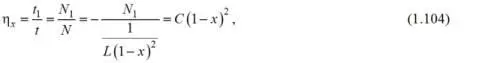Александр Полулях - Грохочение угля

При m=0 имеем p=0 – невозможность, когда ни один случай не благоприятствует наступлению события, при m=n имеем p=1 – достоверность, когда каждый случай благоприятствует событию.

Величина N , обратная вероятности p , определяет вероятное число случаев, при котором данное событие может иметь место

Предположим, что мы имеем сито из бесконечно тонкой проволоки с квадратными отверстиями величиной l . Допустим также, что шарообразные частицы диаметром d при грохочении падают перпендикулярно к плоскости сита. Будем считать, что зерна проходят через отверстия беспрепятственно, если не касаются проволоки, т. е. центр частицы при падении проектируется на заштрихованную площадь (l - d) 2 (рис. 1.20, а ).

Можно считать, что число случаев, благоприятствующих прохождению зерна через отверстие, пропорционально заштрихованной площади (l - d) 2 , а число всех возможных случаев падения частицы на отверстие пропорционального его площади l 2 . Вероятность прохождения зерна через отверстие определится отношением площадей

Тогда величина N , обратная вероятности p , определит вероятное число отверстий, которое необходимо встретить частице, чтобы в одно из них пройти сквозь сито.

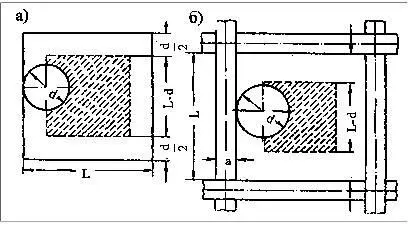
Рис. 1.20. Схема прохождения частицы через отверстие сита

Значения величин p и N для различных отношений d / l приведены в табл. 1.10, по данным которой построен график (рис. 1.21). Из графика видно, что небольшое увеличение диаметра частицы сверх 0,75 l вызывает значительное возрастание числа отверстий для прохождения частицы сквозь сито.

Таблица 1.10

Вероятность прохождения зерна через отверстие в зависимости от его относительного размера

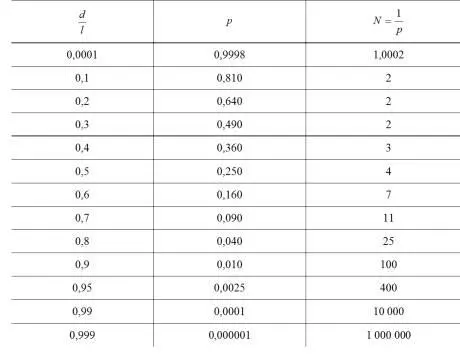
Следовательно, теория вероятностей подтверждает принятое практикой деление частиц на «легкие» (d<0,75l) и «трудные» (d>0,75l) .

Если учесть толщину проволок сита (рис. 1.20, б ), то, рассуждая аналогично предыдущему, получим следующее выражение для вероятности прохождения частицы сквозь сито:

Первый член этого выражения – коэффициент живого сечения сита. Отсюда видно, что вероятность прохождения частицы прямо пропорциональна живому сечению сита.

На основе рассмотренного определения вероятности прохождения частиц сквозь сито можно установить эффективность грохочения частиц диаметром x=d / l (весьма узкого класса).

Согласно формуле (1.101) имеем

где L – коэффициент живого сечения сита в долях единицы.

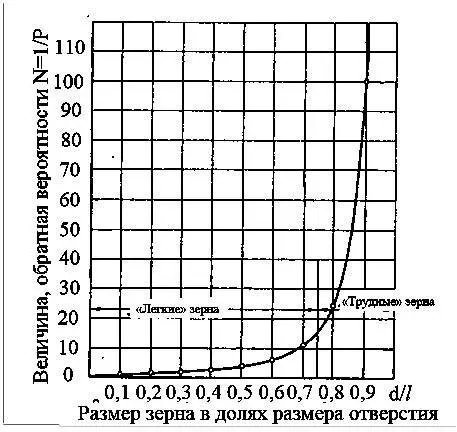
Рис. 1.21. Вероятность прохождения частицы сквозь сито в зависимости от относительного его размера

Число отверстий N , которое надо встретить частицам, составляющим рассматриваемый узкий класс, для полного прохождения сквозь сито, равно

Встреча с этим числом отверстий обеспечивается при определенной продолжительности грохочения t . Если время грохочения t 1 меньше t , то частицы просеваемого узкого класса встретят число отверстий N 1 , меньшее N , и пройдут сквозь сито не полностью. Извлечение этого узкого класса в подрешетный продукт (эффективность грохочения по данному классу)

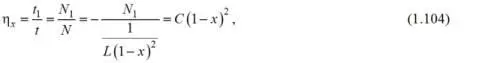
где C – постоянный для данного грохота коэффициент пропорциональности.

Для приближенных подсчетов можно пользоваться эмпирической формулой