Роб Истуэй - Математика для мам и пап - Домашка без мучений

Решение математических задач может быть похоже на взламывание шифра, и эта – прекрасный тому пример. В задаче скрывается тайна, и вы, как детектив Коломбо из известного сериала, получаете кое-какие улики и далее ищете дополнительную информацию. И хотите верьте, хотите нет, подсказок здесь множество. Во-первых, тот факт, что число 4095 – нечетное. Если при перемножении двух чисел ответ получается нечетный, то и оба перемножаемых числа должны быть нечетными. (Надо сказать, это было откровением для одной умненькой учительницы младших классов, с которой нам довелось беседовать, – она никогда не сталкивалась с тем, что четное число при умножении на любое другое целое число обязательно дает четный результат, хотя, стоило ей задуматься, как это стало очевидным.)

Поэтому мы немедленно понимаем, что два числа, о которых идет речь, должны браться из набора 51, 53, 55, 57, 59, 61, 63, 65, 67 и 69. Однако число возможных вариантов еще снижается, если обратить внимание на то, что произведение заканчивается на 5; значит, по крайней мере один из сомножителей тоже заканчивается на 5. Следовательно, одно из чисел должно быть 55 или 65. Быстрая проверка на калькуляторе показывает, что 4095 не делится нацело на 55, зато 4095: 65 = 63, что дает нам второе число.

На самом деле математики, натренированные в решении такого рода примеров, смогут ответить на вопрос без всякого калькулятора. Если вам интересно (а может, и нет!), как они это сделают, читайте дальше. Во-первых, математик посмотрел бы на простые множители числа 4095. Он понял бы, что поскольку число 4095 – нечетное, то оба сомножителя тоже должны быть нечетные. Он сразу же заметил бы, что 4095 делится на 5, а значит, один из сомножителей должен равняться 55 или 65. Затем он заметил бы, что 4095 не делится на 11, то есть число 55 не может быть одним из делителей. Единственным вариантом остается 65. Наконец, математик заметил бы, что 4095 делится на 9, то есть второй делитель должен быть нечетным числом, кратным 9 и лежащим между 50 и 70. Это значит, что второй множитель равен 63.

Не тревожьтесь, если это краткое объяснение не пролило свет на проблему; главный его смысл в том, что при наличии достаточных математических знаний можно найти приемы, которые позволят вам щелкать сложные на первый взгляд примеры как орешки.

Ничто из перечисленного не требуется от ребенка, заканчивающего начальную школу. И все же многие ученики более чем способны понять и использовать эти приемы. Подталкивая детей к исследованию числовых тайн, вы учите их решать задачи быстрее и, главное, помогаете открыть для себя, что математика – не только слепой поиск и метод проб и ошибок: это еще и интереснейшая детективная работа, приключения и открытия.

Э.

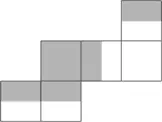
«Задачи на развертки, – признался один учитель начальной школы, – внушают мне ужас. Это мое абсолютное слабое место, моя ахиллесова пята». Ожидается, что учащийся должен уметь мысленно свернуть плоский лист бумаги так, чтобы получился простой трехмерный объект (и представить себе противоположное – как выглядит объемный предмет, если его развернуть на плоскости). И это задача, которую многие дети находят очень-очень сложной. Чтобы понять, что происходит, большинству нужно нарисовать развертку и физически превратить ее в объект. В этот момент они готовы будут кричать: «Эврика!» К несчастью, рисование модели требует времени, и лишь самые отчаянные и организованные из детей справятся с эти меньше чем за пять минут – поэтому такой путь приведет к потере драгоценного экзаменационного времени. Единственный способ обойти эти сложности в том, чтобы заранее развивать у детей способность строить развертки и складывать из них фигуры. Тогда в нужный момент они смогут без труда выполнить это в уме.

MDCLXVI – число 1666, год Большого лондонского пожара. Его можно найти на монументе возле Лондонского моста.

Полезно представлять себе числа в виде суммы его отдельных частей. 124 можно записать как 100 + 20 + 4. Не забывайте, что мы в данном случае работаем в системе счисления с основанием 8, так что 20 означает не двадцать (то есть две группы по 10), а две группы по 8, так что 20 в восьмеричной системе соответствует 16 в десятеричной. 100 в восьмеричной системе обозначает одну группу из 8 групп по 8, то есть 64 в десятеричной системе. Значит, 124 в восьмеричной системе счисления – это 64 + 16 + 4, или 84, в десятичной системе. Запутались? Представьте, как чувствует себя ребенок, когда впервые пытается разобраться в позиционной системе и разрядных значениях.