Роб Истуэй - Математика для мам и пап - Домашка без мучений

Устный счет – отличная тренировка базовых навыков, но может быть, ваш ребенок заинтересуется тем, как и почему это работает. Для объяснения дайте задуманному сыном или дочерью числу какое-то забавное имя (например, Клякса) и представьте, что это число накрепко запечатано в конверт.

• Представь себе число: Клякса .

• Удвой это число. Что получится? Клякса и Клякса (или две Кляксы ), а значит, два конверта с одинаковыми Кляксами внутри.

• Прибавь десять – десять может быть чего угодно, но пусть это будет десять пальцев. Получается две Кляксы плюс десять пальцев.

• Раздели результат на два. Половина от двух Клякс и десяти пальцев – это одна Клякса и пять пальцев.

• Отними задуманное число, то есть Кляксу. От одной Кляксы и пяти пальцев отнять Кляксу, останется пять пальцев.

Иными словами, не имеет значения, с какого числа вы начнете (Клякса), потому что в конце вы от него все равно избавитесь и останетесь только с числом 5 (пальцев).

Мы использовали условную Кляксу для представления произвольного числа, и то, что мы вместе проделали, вообще-то подпадает под формальное определение алгебры, которой учат в средней школе. Просто в школе Кляксе дают куда менее забавное имя – такое как x или y . Взрослые часто жалуются, что в детстве они никогда не понимали, почему числа нужно обозначать буквами. Волшебный фокус с Кляксой – удобный способ показать ребенку, что иногда полезно дать неизвестному числу имя.

Кстати говоря, если вы уже поняли, как работает базовая версия фокуса, вы можете посмотреть, что произойдет, если давать ребенку другие команды. Как можно изменить фокус, чтобы в ответе всегда получалось 6? (Ответ: прибавлять 12 вместо 10.) А если утроить, а не удвоить? Возможности бесконечны.

Математика может заявить о себе самым неожиданным образом. Например, когда раскрашиваешь карту, нежелательно, чтобы два соседних региона получились одного и того же цвета. Так вот, математикам потребовалось более 100 лет, чтобы доказать: для правильного расцвечивания географической карты потребуется не более четырех разных красок (регионы, соприкасающиеся в одной-единственной точке, соседними не считаются и могут быть одного цвета). Проверьте сами: можно раскрасить все области Австралии, используя только красный, зеленый, желтый и синий (для моря) цвета.

А теперь нарисуйте, не отрывая карандаша от бумаги, любые каракули так, чтобы прочерченная линия закончилась в той же точке, где и началась. Получится что-нибудь вроде:

Сколько красок нужно, чтобы раскрасить такую карту? Не более двух – не существует закорючки, для раскрашивания которой не хватит двух красок. Если вы сделаете каракули, скажем, черно-белыми, никакие две соседние области не окажутся одного цвета:

Убедиться в этом и поэкспериментировать может любой ребенок. Но чтобы объяснить данный феномен потребуется более хитроумная математика, известная как теория графов, – очень интересная, но выходящая далеко за пределы программы начальной школы.

Говорят, что старые фокусы – самые лучшие, и это совершеннейшая истина в отношении этого трюка с «чтением мыслей». Напоминания о нем часто можно встретить в рождественских хлопушках с сюрпризом и в детских наборах с фокусами.

Вам потребуется четыре карточки с числами, в точности такие, как показано ниже.

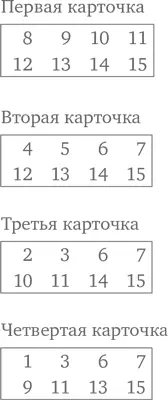
Сценарий таков: «Задумайте число от 1 до 15, но не говорите мне, что это за число. Теперь я покажу вам по очереди четыре карточки, и для каждой задам один и тот же вопрос: „Есть ли здесь ваше число?“ Те карточки, про которые вы скажете „Да“, я буду откладывать в сторону. После того как я покажу вам все четыре, я смогу волшебным образом угадать, какое число вы задумали!»

Чтобы найти задуманное число, возьмите те карты, на которых оно имеется, и сложите числа, расположенные на них в верхнем левом углу .