Роб Истуэй - Математика для мам и пап - Домашка без мучений

Это образец так называемого визуального доказательства, а доказательство – одна из важнейших концепций математики. Идея здесь в том, что вы можете с уверенностью сказать, что для треугольника любой формы в любой точке мира и в любой момент времени – сегодня, в прошлом или в будущем – площадь равна и всегда будет равна половине произведения основания этого треугольника и его высоты. Это очень мощная идея.

В одной старой математической загадке говорится о том, что у фермера Жиля была коза и 120 м ограды. Фермер хочет огородить для своей козы участок, на котором было бы как можно больше травы.

Сначала он пробует огородить территорию в форме равностороннего треугольника со сторонами по 40 м (тогда периметр составит как раз 120 м).

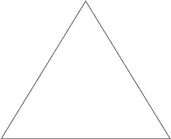
Площадь такого треугольника чуть меньше 700 м2 (основание треугольника равно 40 м, а высота оказывается примерно равной 35 м).

Можно ли сделать лучше? Фермер разворачивает свои 120 м ограды в квадрат 30 × 30 м.

Теперь площадь равна 30 × 30 = 900 м2. Получается, что если у вас имеется ограда определенной длины, то площадь квадратного поля, окруженного этой оградой, окажется больше, чем площадь поля треугольного.

Далее фермер пробует правильный шестиугольник, каждая сторона которого равна 20 м.

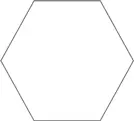
Теперь площадь поля составляет приблизительно 1039 м2 (один из способов вычислить эту площадь состоит в том, чтобы найти площадь одного сегмента шестиугольника, представляющего собой равносторонний треугольник, и умножить на 6).

Таким образом, при заданной длине ограды площадь, судя по всему, получается тем больше, чем больше сторон у вашего поля.

Пройдите в этом направлении дальше и рассмотрите поля в форме декагона (10 сторон) и икосагона (20 сторон); по мере увеличения числа сторон форма поля Жиля начинает напоминать круг. На самом деле круг – многоугольник с бесконечным числом сторон, и если фермер использует свои 120 м ограды для создания круглого поля, он сможет огородить почти 1150 м2 пастбища – намного больше, чем было в первоначальном треугольнике, и, мало того, максимально возможная площадь, которую Жиль может огородить. Это лишь одно из многих важных свойств круга, которыми объясняется его особая роль в геометрии.

Кстати говоря, на идее получать ответ, выбирая все более мелкие шаги и переходя в конце концов к шагам бесконечно малым, построена одна из важнейших областей высшей математики, известная как дифференциальное исчисление. Наши представления о высшей математике чуть ли не всем обязаны дифференциальному и интегральному исчислению, и мы должны благодарить Исаака Ньютона (и других) за идеи о математике бесконечно малых величин. Что подводит нас к еще одной, заключительной теме нашей книги…

Когда ваши дети будут смотреть мультсериал «Историю игрушек» или играть с фигуркой его главного героя, Базза Лайтера, задайте им вопрос по поводу его коронной фразы: «В бесконечность и дальше». Идея бесконечности начинает интересовать детей уже в пяти– или шестилетнем возрасте, потому что это «самое большое» возможное число. Это так или нет? Базз Лайтер, судя по всему, фактом своего существования утверждает, что можно проникнуть дальше бесконечности.

Само собой, бесконечность – странная идея, и вы поможете детям осознать ее, рассказав им, например, историю гостиницы Гилберта.

В гостинице Гилберта было бесконечное число комнат. Невероятно, но однажды ночью отель заполнился под завязку. В каждой из комнат под номерами 1, 2, 3, 4 и так до бесконечности кто-то остановился. Затем в дверь гостиницы постучал еще один человек и спросил: «Есть у вас комната?» Управляющий подумал немного и ответил: «Вам повезло, есть». Он послал всем своим постояльцам такое сообщение: «Пожалуйста, переселитесь в комнату с номером на единицу больше номера вашей нынешней комнаты». Человек из номера 1 переехал в номер 2, из номера 2 – в номер 3, из 3 – в 4 и т. д. Понятно, что у постояльца из любого номера, какой только можно представить, даже самого большого, найдется номер на единицу больше. Так что у каждого теперь есть комната, и все комнаты полны – за исключением номера 1, который теперь пуст. Управляющий вручает ключ от номера 1 новому постояльцу.