Всегда ли работает такое сложение? Чему, как вы полагаете, равно 102 × 104? Если правило сложения работает, то в ответе должно получиться 106, поскольку 2 + 4 = 6 – и быстрая проверка показывает, что это верный ответ (100 × 10 000 = 1 000 000, или миллион).
Таким образом, при помощи логарифмов можно без труда превратить умножение в сложение. И это работает при любом основании. То есть 32 × 34 = 36 (2 + 4 = 6). Если записать полностью, то получится, что мы 3 × 3 (9) умножаем на 3 × 3 × 3 × 3 (81), и получается 3 × 3 × 3 × 3 × 3 × 3 (729). Это оказывается весьма полезным, когда числа становятся слишком большими для калькулятора. Так что теперь вы можете уверенно сказать, что 179 × 174 равно 1713, хотя при попытке проверить это утверждение при помощи электроники вы, вероятно, получите лишь сообщение об ошибке.
Далее. Если ваш ребенок готов признать, что такое правило сложения – штука хорошая и удобная и что правило это, судя по всему, работает всегда, вы можете воспользоваться ситуацией и расширить идею о применении степеней. Что такое 30? Большинство детей (да и большинство взрослых), скорее всего, скажет, что это нуль, но если вы усвоили, что правило сложения работает всегда, то 30 должно равняться 1. Почему? Посмотрите, скажем, на пример 30 × 32. Согласно правилу сложения степеней 0 + 2 = 2, так что ответ должен равняться 32 или, иными словами, 30 × 9 = 9… что означает, что 30 должно равняться 1. Более того, по этому правилу любое число в нулевой степени равняется 1!
Здесь не обойтись без некоторого осмысления, поэтому стоит остановиться и дать мальчику или девочке время освоиться с новыми идеями. Но на всякий случай – если вам или вашему ребенку не терпится двигаться дальше – добавим, что правило сложения степеней работает также для дробей и отрицательных чисел. К примеру, 101/2 – это квадратный корень из 10 (примерно 3,16), потому что 101/2 × 101/2 = 101. А что с отрицательными числами? 10–1 равно 0,1, или одной десятой, потому что 10–1 × 101 = 100 = 1. Очень хорошо, хватит!!!
Все это весьма серьезные идеи, и вполне возможно, что для многих ребят некоторые из них окажутся слишком серьезными. Но не забывайте, что очень большие числа, как правило, завораживают детей. Тот факт, что для записи числа, при помощи которого можно выразить размер Вселенной, достаточно всего трех или четырех цифр (к примеру, 1091), – интересная математическая загадка, которой имеет смысл поделиться.
Как найти площадь треугольника
Вернемся вновь к обычным повседневным числам. Ранее (см. «Площади более сложных фигур») мы описывали способ определения приблизительной площади треугольника при помощи подсчета квадратиков. Но, как известно многим родителям, существует и точная формула для вычисления площади треугольника. Возможно, вы помните формулировку: «Половина основания умножить на высоту».
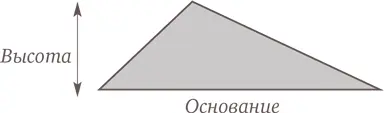
Таким образом, если основание изображенного здесь треугольника – 6 м, а высота – 3 м, то площадь данной фигуры составит 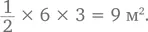
Но почему площадь треугольника всегда равна половине основания, умноженной на высоту? Мало кто из родителей знает, чем это объясняется, большинство просто помнит правило.
На самом деле все очень просто, и если вы сами это поймете, то сможете просветить и своих детей. Возьмите произвольный треугольник и представьте, что располагаете его так, чтобы самая длинная его сторона оказалась внизу.
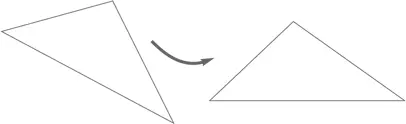
А теперь представьте, что помещаете свой треугольник внутрь тесного ящика и проводите вертикальную линию от верхней вершины треугольника к основанию.
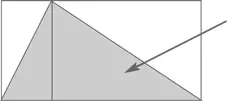
Каждая часть треугольника представляет собой половину соответствующего прямоугольника, так что полная площадь будет составлять половину от площади всего прямоугольника – иными словами, половину произведения его основания на высоту.
Поместите два таких треугольника рядом. Промежуток между ними всегда будет представлять собой первоначальный треугольник, перевернутый вверх ногами, поэтому треугольники будут аккуратно вписываться в прямоугольную полосу, которая может продолжаться до бесконечности.
Читать дальше
Конец ознакомительного отрывка
Купить книгу


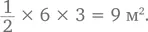









![Роб Истуэй - Математика на ходу [Более 100 математических игр для больших и маленьких] [litres]](/books/406847/rob-istuej-matematika-na-hodu-bolee-100-matematich-thumb.webp)



