• А теперь, втайне приготовившись нажать на «квадратный корень», попросите ребенка задуть свечи. При первой попытке потихоньку нажмите кнопку – 3, 9 и 0 исчезнут с экрана, оставив 625. Попросите дунуть еще раз. На этот раз исчезнет шесть. Еще раз – пропадет 2. Попросите дунуть еще один, последний, раз – особенно сильно – и незаметно перенесите палец на кнопку выключения калькулятора. Экран очистится. (Иногда у калькуляторов на солнечных батареях нет кнопки выключения. В этом случае единственный способ убрать все с экрана – полностью затемнить комнату!)
Объяснение этого фокуса заключается в необычном свойстве чисел 5, 25 и 625: когда их возводишь в квадрат, они появляются в конце получившегося числа.
Игра: «Шесть-один-шесть»
В эту игру можно играть и без калькулятора, но на последующих этапах в ней можно использовать более сложный калькулятор.
Подготовьте три карточки с числами 1, 6 и 6 (единица должна выглядеть как простая вертикальная черта). Попросите ребенка составить из этих карточек самое большое число, какое только можно. Затем, когда это будет сделано, предложите составить самое маленькое возможное число.
Вполне может быть, что ребенок предложит в качестве наибольшего числа 661, а наименьшего – 166. Бесспорно, это хорошие ответы. Но на самом деле здесь есть большой простор для творчества. Что, если перевернуть 6 вверх ногами? Она превратится в 9, и можно будет предложить в качестве наибольшего числа 991.
Этого мало. Что, если положить 1 на бок? Теперь можно наименьшим объявить число 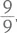 что равно 1. Или, если рассматривать 1 как минус, можно получить 9 – 9 = 0. И даже что-нибудь меньше нуля (если считать, что отрицательные числа меньше нуля), к примеру, – 99. А если вы действительно хотите стимулировать мышление ребенка и считаете, что он для этого готов, вы можете даже подкинуть ему идею степеней. 92 означает 9 × 9, точно так же 96 означает 9 × 9 × 9 × 9 × 9 × 9. Следовательно, если вы хотите получить по-настоящему большое число, вы можете написать 991; это число настолько большое, что оно больше количества атомов во Вселенной. При этом минимум, который вы можете получить, равен –99, что соответствует –387 млн. Такое число заставит поволноваться любой банк.
что равно 1. Или, если рассматривать 1 как минус, можно получить 9 – 9 = 0. И даже что-нибудь меньше нуля (если считать, что отрицательные числа меньше нуля), к примеру, – 99. А если вы действительно хотите стимулировать мышление ребенка и считаете, что он для этого готов, вы можете даже подкинуть ему идею степеней. 92 означает 9 × 9, точно так же 96 означает 9 × 9 × 9 × 9 × 9 × 9. Следовательно, если вы хотите получить по-настоящему большое число, вы можете написать 991; это число настолько большое, что оно больше количества атомов во Вселенной. При этом минимум, который вы можете получить, равен –99, что соответствует –387 млн. Такое число заставит поволноваться любой банк.
Подробнее о степенях мы поговорим в следующей главе.
Большие идеи для маленьких человечков

Большая часть этой книги посвящена тем аспектам математики, с которыми ваш ребенок впервые познакомится в начальной школе. Но как быть с действительно серьезными областями математики – алгеброй, геометрией, логарифмами, представлениями о бесконечности? Это для старшей школы, не правда ли? Действительно, школьная программа помещает эти вопросы именно туда (и вы найдете их в нашей книге «Больше математики для мам и пап»), но на самом деле в «высшей математике» существует множество идей, которые будут не только понятны, но и интересны умненькому десятилетнему ребенку. В этой главе мы предложим вам семь способов (включая «волшебные») познакомить детей с некоторыми аспектами высшей математики.
Задумай число (волшебство алгебры)
– Задумай число, любое, какое захочется (но вам, возможно, захочется, чтобы оно было меньше десяти).
– Удвой это число.
– Прибавь к нему 10.
– Раздели на два.
– Наконец отними от того, что получилось, задуманное число.
– А теперь мы волшебным образом отгадаем, что в конце концов из всего этого получилось… 5!
Разумеется, именно столько должно было получиться.
Дети обожают этот фокус, потому что в нем что-то есть от чтения мыслей. (Но будьте осторожны, дети младше девяти лет запросто могут ошибиться в устных подсчетах, и ответ у них получится другой, что сведет на нет все ваше волшебство.) Они будут просить повторять его снова и снова, пытаясь вас «поймать» и понять, как вы это делаете. Они пробуют и пробуют, и в какой-то момент им может показаться, что вот нашлось число, на которое волшебство не действует. Конечно, это всегда сводится к арифметической ошибке (поэтому, если у ребенка получилось не 5, попросите его назвать задуманное число и пройдите вместе с ним все этапы, а затем с улыбкой «обнаружьте», что на самом деле из этого числа тоже должно было получиться 5). И в самом деле, в таких случаях всегда получается 5, даже если начать с дробного, отрицательного или просто большого числа.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

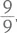 что равно 1. Или, если рассматривать 1 как минус, можно получить 9 – 9 = 0. И даже что-нибудь меньше нуля (если считать, что отрицательные числа меньше нуля), к примеру, – 99. А если вы действительно хотите стимулировать мышление ребенка и считаете, что он для этого готов, вы можете даже подкинуть ему идею степеней. 92 означает 9 × 9, точно так же 96 означает 9 × 9 × 9 × 9 × 9 × 9. Следовательно, если вы хотите получить по-настоящему большое число, вы можете написать 991; это число настолько большое, что оно больше количества атомов во Вселенной. При этом минимум, который вы можете получить, равен –99, что соответствует –387 млн. Такое число заставит поволноваться любой банк.
что равно 1. Или, если рассматривать 1 как минус, можно получить 9 – 9 = 0. И даже что-нибудь меньше нуля (если считать, что отрицательные числа меньше нуля), к примеру, – 99. А если вы действительно хотите стимулировать мышление ребенка и считаете, что он для этого готов, вы можете даже подкинуть ему идею степеней. 92 означает 9 × 9, точно так же 96 означает 9 × 9 × 9 × 9 × 9 × 9. Следовательно, если вы хотите получить по-настоящему большое число, вы можете написать 991; это число настолько большое, что оно больше количества атомов во Вселенной. При этом минимум, который вы можете получить, равен –99, что соответствует –387 млн. Такое число заставит поволноваться любой банк.







![Роб Истуэй - Математика на ходу [Более 100 математических игр для больших и маленьких] [litres]](/books/406847/rob-istuej-matematika-na-hodu-bolee-100-matematich-thumb.webp)



