Кроме того, число 360 весьма близко к количеству дней в году, так что имело бы смысл обозначить жизненный цикл красивым целым числом, которое представляло бы календарь.
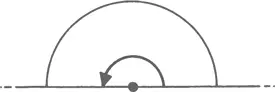
Если 360° – это полная окружность, то половина окружности должна соответствовать 180° :
Прямые, острые и тупые углы
Четверть окружности составляет угол величиной 90°, который известен как прямой угол; обозначается такой угол маленьким квадратиком возле его вершины:
Углы меньше 90° называются острыми, больше 90° – тупыми. (Для полноты отметим, что угол больше 180° иногда называют «отраженным» – хотя вам вряд ли удастся найти много людей, которым это известно.)
Игра: охота за прямоугольными сокровищами
Можно организовать дома охоту за прямоугольными сокровищами. Для этого нужно сделать надежный «пробник» для прямых углов: просто возьмите лист бумаги и сложите его пополам:
Затем сложите его еще раз, так чтобы края на первом сгибе в точности совпали.
Угол, получившийся в том месте, где сходятся линии сгиба, является практически прямым. Таким «инструментом» можно проверять углы, которые кажутся (или должны по идее быть) прямыми, – действительно ли они прямые?
Треугольники бывают трех типов, и считается, что ваш ребенок должен быть знаком со всеми тремя:
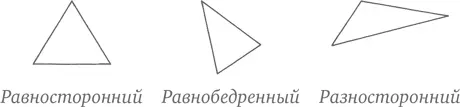
• Равносторонний треугольник – тот, у которого все три стороны (и все три угла) одинаковые.
• Равнобедренный – треугольник с двумя одинаковыми сторонами (и двумя углами).
• В разностороннем – все стороны (и все углы) разные.
У треугольников есть одна занятная особенность: если взять треугольник и измерить у него все три внутренних угла при помощи транспортира, их сумма всегда будет составлять 180°. Существует простой способ убедиться в этом: нужно нарисовать треугольник на листе бумаги, вырезать его, оторвать от него все три угла и сложить их вместе.
Это означает, что если вам известны любые два угла треугольника, вы можете определить, чему равен третий угол. К примеру, если два угла треугольника составляют 30° и 80°, то третий должен быть 180° – (30° + 80°), то есть 70°. И оказывается, что этот маленький кирпичик знания лежит в фундаменте огромного количества куда более хитрой геометрии в составе высшей математики – достаточная причина для того, чтобы ваши дети прочно усвоили данное правило.
Проверьте себя
32. Прямоугольный треугольник
Сара нарисовала треугольник, и один из его углов оказался прямым. Какого типа может быть такой треугольник?
а. Равносторонний
б. Равнобедренный
в. Разносторонний
Проверьте себя
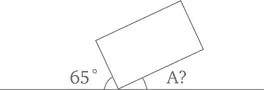
33. Припаркованный автомобиль
Чему равен угол A между автомобилем и стеной?
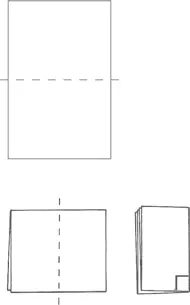
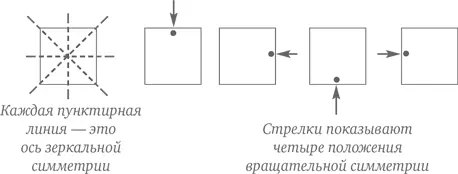
Природа полна симметрии, и математика тоже, и поскольку базовые идеи в этой области просты для понимания, не удивительно, что симметрия достаточно широко представлена в программе по математике для начальной школы. Вот два основных связанных с симметрией понятия, которые ваш ребенок, вероятно, должен будет постичь:
• зеркальная симметрия, при которой одна половина фигуры представляет собой зеркальное отражение другой половины;
• вращательная симметрия, при которой фигура после частичного поворота идентична самой себе.
Все правильные фигуры, описанные ранее в этой главе, имеют столько симметрий, сколько у них сторон; квадрат, к примеру, имеет четыре оси зеркальной симметрии и четыре вращательных симметрии (см. рисунок):
Правильный пятиугольник имеет пять симметрий, шестиугольник – шесть, и т. д.
Читать дальше
Конец ознакомительного отрывка
Купить книгу















![Роб Истуэй - Математика на ходу [Более 100 математических игр для больших и маленьких] [litres]](/books/406847/rob-istuej-matematika-na-hodu-bolee-100-matematich-thumb.webp)



