Роб Истуэй - Математика для мам и пап - Домашка без мучений

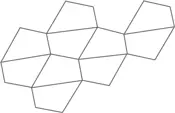
…и до эмблемы из сериала «Звездный путь» (если, конечно, у нее будут прямые стороны):

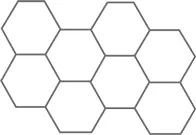
Из правильных шестиугольников тоже получается отличное плотное покрытие (любая пчела может рассказать вам об этом).

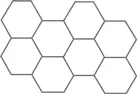
Правильные пятиугольники не годятся для мощения – между ними остается некрасивая щель:

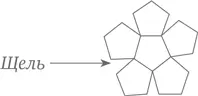
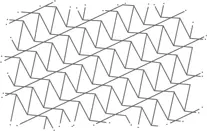
…а вот некоторые неправильные пятиугольники допускают мощение. У такого пятиугольника две его стороны должны быть параллельны друг другу. К примеру:

При мощении подобного рода фигурами образуется интересный, почти трехмерный эффект на плоской поверхности:

Формочки для вырезания печенья обычно бывают круглыми, из-за чего остается много обрезков теста, которые потом приходится месить и раскатывать заново. Почему бы вместо этого не сделать печенье в форме геометрических фигур, пригодных для мощения? В наши дни можно найти формочки для печенья в форме треугольника, ромба и даже шестиугольника. Так что лучше делать шестиугольное печенье, не оставляя обрезков (разве что по периметру). То же самое можно сделать из пластилина, но намного приятнее работать, если конечный продукт предполагается съесть.

Представьте себе пол, выложенный шестиугольными плитками. Плитки скольких цветов вам потребуются, чтобы никакие две соседние плитки не оказались одного и того же цвета?

Равносторонние треугольники, квадраты и пятиугольники можно соединять между собой, чтобы образовать из них объемные фигуры, известные как платоновы тела. Всего таких тел пять. Три из них состоят из треугольников:

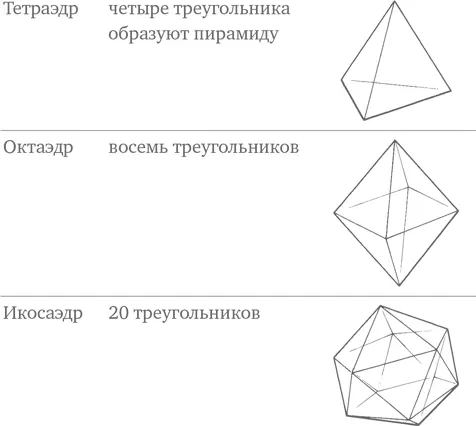
(«-Эдр» – от греческого hedra, «сиденье», означает плоскую грань объемной фигуры.)

Два других платоновых тела:

Складывание из бумаги объемных фигур входит в программу по математике в начальной школе. К семилетнему возрасту ваш ребенок, вероятно, успел уже познакомиться с так называемыми развертками, наверняка ведь ему случалось развернуть картонную коробку, да и в наборах различных конструкторов детям часто предлагается складывать объемные фигуры из деталей-многоугольников. К 11 годам ребенок должен уметь строить развертки не только кубов, но и призм (к примеру, треугольных коробочек), а также других правильных объектов.

Здесь представлены две развертки, из которых можно сложить куб:

Но изготовление развертки куба не сводится к тому, чтобы произвольным образом соединить шесть квадратов. К примеру, из этой развертки не получится полного куба:

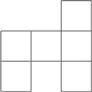
Как ее ни складывай, две грани обязательно наложатся друг на друга.

Вы с легкостью представляете себе, как все это происходит? Если да, вам повезло. Дети в большинстве своем (и многие родители) могут определить, получится ли из развертки объемная фигура, только после того, как физически сложат бумагу по стыкам; именно в этот момент обычно приходит озарение. В классе учащимся, как правило, дают возможность – и время – складывать свои развертки. Однако во время тестов все придется проделывать в голове. Научиться этому можно только на практике.