Кит Йейтс - Математика жизни и смерти. 7 математических принципов, формирующих нашу жизнь

Чтобы лучше понять, как работает регрессия к среднему, рассмотрим результаты экзамена. Возьмем крайний случай, когда студентам предлагается ответить на 50 вопросов с ответами «да» или «нет» по предмету, о котором они ничего не знают. Если студенты будут выбирать ответы исключительно наугад, результаты теста будут варьироваться от нуля до 50, но тех, кто угадает почти все правильно, будет совсем немного – как и тех, кто не угадает почти ничего. Из распределения баллов, приведенного на рис. 20, видно, что средний балл большинства экзаменуемых будет ближе к среднему арифметическому значению 25. Если проанализировать баллы тех, кто попал в 10 % лучших, то они по определению будут значительно выше, чем в среднем по всей группе. Но покажут ли они результаты значительно выше среднего, если их протестировать повторно, со свежими вопросами? Конечно, нет. Мы будем вновь ожидать, что их оценки равномерно распределятся вокруг среднего балла 25. То же самое будет верно и при перепроверке нижних 10 %. Набравшие экстремально высокие и экстремально низкие баллы в первом тесте во втором, как правило, вернутся к среднему показателю.

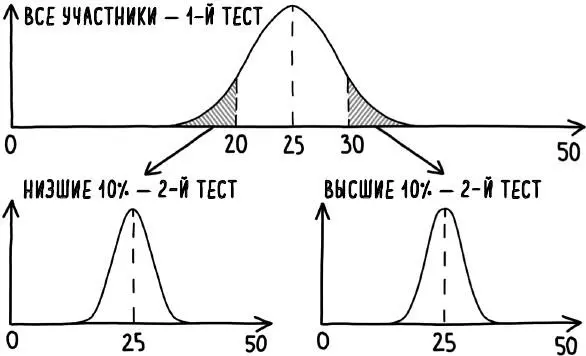
Рис. 20. Распределение баллов при прохождении теста из 50 вопросов с многовариантными ответами «да/нет». При повторном тестировании тех, кто набрал наивысшие 10 % баллов (заштрихованная область справа), их средний балл совпадает со средним общим баллом. То же самое относится к низшим 10 % (заштрихованная область слева). Группы, получившие как высшие, так и низшие баллы, регрессировали в сторону среднего значения

Результат реальных экзаменов в значительной степени будет определяться навыками и трудовой этикой, однако нельзя исключать и элемент везения, который проявляется как в наборе вопросов, выпадающих на экзамене, так и в приоритетности предметов для повторного экзамена. Регрессия к среднему способна выявить такой эффект – если он имел место. Элемент случайности особенно заметен на экзаменах с многовариантным набором ответов, из которых даже студент, не обладающий необходимыми знаниями, может угадать правильный. В одном исследовании, проведенном в 1987 году, 25 подверженных «экзаменационной панике» американских студентов, которые неожиданно плохо справились с тестом на проверку академических способностей (SAT), прошли повторное тестирование, предварительно приняв пропранолол – лекарство от гипертонии [134] Faigel, H. C. (1991). The effect of beta blockade on stress-induced cognitive dysfunction in adolescents. Clinical Pediatrics, 30 (7), 441–5. https://doi.org/10.1177/000992289103000706 . Газета New York Times сообщала о результатах исследования так: «Препарат, используемый для лечения высокого кровяного давления, резко улучшил результаты теста на проверку академических способностей у студентов, страдающих от необычайно сильной тревожности…». Студенты, принимавшие пропранолол, значительно повысили свои оценки – в среднем на 130 баллов по шкале от 400 до 1600. Поначалу кажется, что пропранолол – невероятно действенное средство. Оказывается, однако, что даже ученики, которые не нервничали перед тестом, при повторной сдаче улучшают свои оценки примерно на 40 баллов. Если учесть, что студенты, отобранные для исследования, были выбраны именно потому, что они показали результаты хуже, чем предполагалось по их IQ или другим академическим показателям, они вполне могли бы и без пропранолола значительно повысить свои баллы в результате регрессии к среднему.

Без контрольной группы студентов, получивших такие же низкие баллы на первом тесте и прошедших переэкзаменовку без препарата, эффект его воздействия определить нельзя. Очень соблазнительно было бы приписать прогресс студентов воздействию пропранолола, основываясь только на результатах получавшей его группы. Однако итоги случайного теста с многовариантными ответами показывают, что регрессия групп, показавших экстремальные результаты, к среднему значению является чисто статистическим феноменом.

В медицинских исследованиях очень важно не путать причину со следствием (не говоря уже о подтасовке причинно-следственных связей). Один из способов предотвратить это (как мы уже видели в главах 2 и 3) – рандомизированное контролируемое исследование, в котором пациенты распределяются случайным образом по двум группам. Как и в исследовании тамоксифена (средства от рака груди), пациенты в группе лечения получают настоящую терапию, а пациенты в контрольной группе – плацебо. Если и пациенты, и организаторы не знают, в какой из групп находится конкретный пациент, исследование называют двойным слепым. Это считается золотым стандартом клинических испытаний. При двойном слепом рандомизированном контролируемом исследовании любая разница между улучшением в контрольной группе и улучшением в группе лечения может быть надежно отнесена исключительно на счет лечения, исключая регрессию к среднему.