Кит Йейтс - Математика жизни и смерти. 7 математических принципов, формирующих нашу жизнь

Первой ошибкой Мидоу было предположение, что случаи синдрома внезапной детской смерти являются полностью независимыми событиями. Эта ложная посылка позволила ему при расчете вероятности того, что смерть двух детей в одной семье будет вызвана СВДС, просто перемножить число 8543 на самое себя. В результате он получил, что вероятность такого события составит примерно 1 на каждые 73 миллиона удачных родов. Пытаясь обосновать свои предположения, он даже заявил: «Нет никаких доказательств того, что “смерти в колыбели” происходят в семьях серийно, зато серийному жестокому обращению с детьми доказательств множество». С этой цифрой на руках он предположил, что при уровне рождаемости в Великобритании, составляющем около 700 тысяч человек в год, две подряд «смерти в колыбели» можно было бы ожидать примерно раз в 100 лет.

Его допущение было исключительно некорректным. Известно много факторов повышения риска СВДС. В их число входят курение, преждевременные роды и даже сон в одной постели с родителями. В 2001 году исследователи Манчестерского университета выделили генетические маркеры, связанные с регулированием иммунной системы, которые также повышают риск СВДС [92] Summers, A. M., Summers, C. W., Drucker, D. B., Hajeer, A. H., Barson, A., & Hutchinson, I. V. (2000). Association of IL-10 genotype with sudden infant death syndrome. Human Immunology, 61 (12), 1270–73. https://doi.org/10.1016/S0198–8859 (00) 00183-X . С тех пор обнаружили множество других генетических факторов, также увеличивающих вероятность СВДС [93] Brownstein, C. A., Poduri, A., Goldstein, R. D., & Holm, I. A. (2018). The genetics of Sudden Infant Death Syndrome. In SIDS: Sudden Infant and Early Childhood Death: The Past, the Present and the Future. Dashash, M., Pravica, V., Hutchinson, I. V., Barson, A. J., & Drucker, D. B. (2006). Association of Sudden Infant Death Syndrome with VEGF and IL-6 Gene polymorphisms. Human Immunology, 67 (8), 627–33. https://doi.org/10.1016/J.HUMIMM.2006.05.002 . У родных братьев и сестер много общих генов – соответственно, риск развития СВДС у них выше. Если от СВДС умирает один ребенок, то вполне вероятно, что в семье действуют какие-то сопутствующие факторы риска. Следовательно, вероятность второй смерти в такой семье будет выше, чем в среднем по населению. В действительности считается, что в Великобритании ежегодно происходит хотя бы один случай СВДС у второго ребенка.

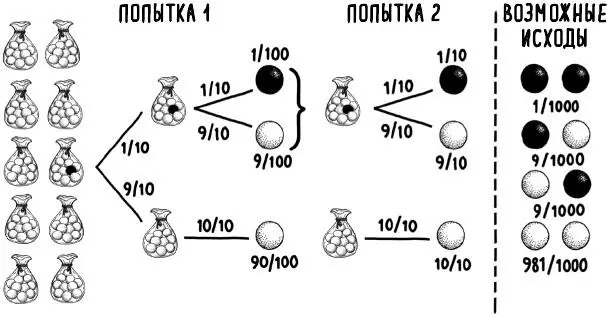
Рис. 9. Древо решений для поиска вероятности выбора черных или белых шариков. Для вычисления вероятности выбора черного или белого шарика при каждой попытке следуйте за соответствующими ветвями древа и умножайте вероятности на каждом шаге. Так, вероятность вытащить черный шарик с первой попытки составляет 1/100. При второй попытке мы выбираем из того же мешка, который мы выбрали при первой попытке. Вероятности каждой комбинации из двух вариантов показаны справа от пунктирной линии

Давайте смоделируем ситуацию, в которой мы сможем вычислить аналог вероятности смерти от СВДС. Возьмем десять мешочков с мраморными шариками. В девяти таких мешочках по десять белых шариков. В десятом же – девять белых и один черный. Эти стартовые условия представлены слева на рис. 9. На первом шаге вы выбираете произвольный мешок, а в нем – произвольный шарик. Поскольку шариков всего 100 и выбор любого из них одинаково возможен, вероятность выбора черного шарика на первом шаге составляет 1 из 100. На втором шаге вы возвращаете шарик обратно в тот же мешочек и вытаскиваете из него же еще один, игнорируя остальные мешочки. Если на первом шаге вы вытянули черный шарик, то вы знаете, что и во второй раз выбираете из набора, в котором этот шарик точно есть. Это значительно повышает вероятность выбора черного шарика – до 1 из 10, а не 1 из 100. В этом сценарии выбор двух черных шариков подряд (с вероятностью 1 к 1000) намного более вероятен, чем при простом перемножении исходной вероятности выбора одного черного шарика на саму себя (что даст вероятность удачного исхода в 1 к 10 000). В случае с вероятностью смерти второго ребенка от СВДС, если первый умер от этого синдрома, математика аналогична – вероятность растет.

При реальном расчете угрозы СВДС факторы риска для каждой семьи не выбираются случайным образом из всего их многообразия; они уже заданы заранее – можно утверждать, что с самого начала вы либо выбираете из мешочка с черным шариком в нем, либо из другого, в котором черного шарика заведомо нет. Эта альтернативная интерпретация проиллюстрирована в виде двух деревьев принятия решений на рис. 10. Если вам достался мешочек с черным шариком в обоих случаях, то вероятность выбора двух черных шариков возрастает до 1 к 100. Таким образом очевидно, что простое перемножение общепопуляционного фактора фонового риска развития СВДС на самого себя при вычислении вероятности развития СВДС для конкретного случая – некорректный прием.