Кит Йейтс - Математика жизни и смерти. 7 математических принципов, формирующих нашу жизнь

Гауссова кривая, или кривая нормального распределения, с помощью которой можно описывать самые разные обыденные наборы данных – от роста до показателей IQ, – выглядит как гармоничная симметричная кривая, в которой половина данных лежит на одной стороне среднего значения, а половина – на другой. Это означает, что среднее и медианное – среднее значение распределения данных – значение характеристик, которые подчиняются этому распределению, склонны совпадать. Привыкнув к тому, что эту замечательную кривую можно использовать для описания реальных событий и явлений, многие из нас предполагают, что понятие «среднего» является хорошим маркером «середины» набора данных. Столкновение же с распределениями, где среднее значение не совпадает с медианным, может нас ошарашить. Распределение возраста смерти британских мужчин, показанное на рис. 11, явно далеко от симметрии. Поэтому подобные распределения обычно называют «смещенными» или «асимметричными».

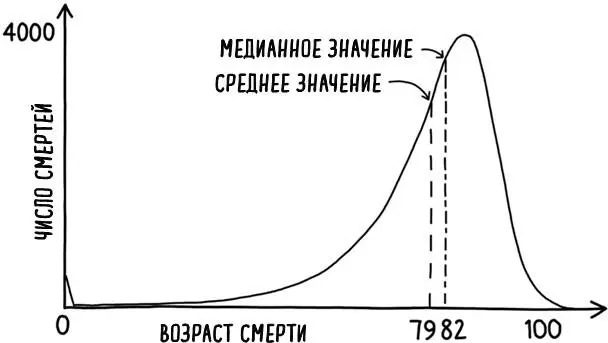
Рис. 11. Возрастная зависимость числа смертей в год у мужчин в Великобритании следует искаженному распределению. Средний возраст смерти составляет чуть менее 79 лет, в то время как медианный возраст – 82 года

Как мы видели в предыдущей главе (где познакомились с медианой, обсуждая способы предотвратить ложные срабатывания сигнала тревоги), распределение доходов домохозяйств – это еще один статистический показатель, медианное значение которого сильно отличается от среднестатистического. Распределение доходов домохозяйств в Великобритании, показанное на рис. 4, также асимметрично; та кривая очень напоминает изломанную и зеркально отображенную версию кривой на рис. 11. Большинство домохозяйств Великобритании имеют низкий располагаемый доход, но есть небольшое, но статистически значимое число богатых, которое искажает симметрию распределения. В 2014 году недельные доходы двух третей британцев были ниже «среднего» уровня.

Поначалу еще более удивительным примером кажется старая загадка: «Каков шанс на то, что у следующего человека, которого вы встретите на улице, ног будет больше, чем в среднем у людей?» Ответ: «Почти наверняка». Соль в том, что одноногих или вовсе безногих калек очень немного, но они и обеспечивают некоторое снижение среднего количества ног в пересчете на все население. Так что каждый, у кого две ноги, имеет больше ног, чем все население в среднем. Этот пример показывает, насколько смехотворны попытки оценивать индивидуальные качества, исходя из усредненных показателей по всей популяции.

Очевидно, что использование некорректного усреднения для описания популяции может привести к экологическим ошибкам. Еще один тип экологической ошибки, известный как парадокс Симпсона, возникает, когда мы пытаемся взять среднее значение из двух и более разнородных групп данных. Парадокс Симпсона проявляется в самых разных областях – от оценки состояния экономики [94] Ma, Y. Z. (2015). Simpson’s paradox in GDP and per capita GDP growths. Empirical Economics, 49 (4), 1301–15. https://doi.org/ 10.1007/s00181-015-0921-3 до интерпретации социально-демографических электоральных профилей [95] Nurmi, H. (1998). Voting paradoxes and referenda. Social Choice and Welfare, 15 (3), 333–50. https://doi.org/10.1007/s003550050109 и, что, возможно, наиболее важно, в разработке лекарств [96] Abramson, N. S., Kelsey, S. F., Safar, P., & Sutton-Tyrrell, K. (1992). Simpson’s paradox and clinical trials: What you find is not necessarily what you prove. Annals of Emergency Medicine, 21 (12), 1480–82. https://doi.org/10.1016/S0196-0644 (05) 80066-6 . Представьте себе, например, что мы отвечаем за контролируемое испытание нового препарата для снижения давления «Фантастикол». На исследование записалось 2000 добровольцев обоих полов, причем количество мужчин и женщин получилось равным. В целях контроля мы разделили их на две группы по 1000 человек. Пациенты в группе А получат «Фантастикол», а пациенты в группе Б – плацебо. В конце исследования выяснилось, что у 56 % (560 из 1000) человек, получавших препарат, артериальное давление снизилось, а в группе получавших плацебо этот эффект наблюдался только у 35 % (350 из 1000) добровольцев (см. таблицу 5). Похоже, что «Фантастикол» действительно работает.

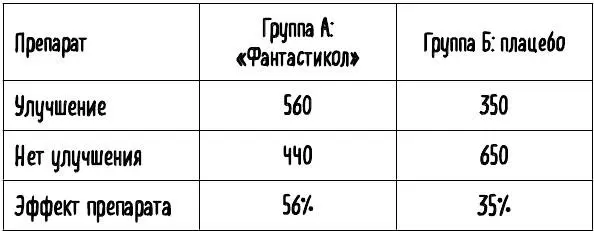
Табл. 5. «Фантастикол», похоже, оказывает в целом более существенный благоприятный эффект, чем плацебо

Для правильной адресации препарата важно знать особенности его воздействия с учетом половой принадлежности пациента. Следовательно, нам нужно понять, как наш препарат действует на мужчин и женщин по отдельности, поэтому мы перераспределяем наши статистические данные соответственно. Эта более подробная разбивка приведена в табл. 6. Анализ результатов оказывается несколько неожиданным. У мужчин из группы Б, принимавших плацебо, артериальное давление понизилось у 25 % (200 из 800 в группе Б), а вот у мужчин из группы А, принимавших «Фантастикол», такой же благотворный эффект наблюдался лишь в 20 % случаев (40 из 200). Среди женщин очевидна та же тенденция: в группе Б давление понизилось в 75 % случаях (150 из 200), а в группе А – только в 65 % случаев (520 из 800). Для обоих полов доля тех, на ком плацебо сказался благотворнее, чем «Фантастикол», оказывается выше. В этом свете новый препарат уже кажется менее эффективным, чем плацебо. Как может быть, что при разбиении данных на группы и их стратификации исследование рассказывает одну историю, а при объединении групп – противоположную, и какая из этих историй правдива?