Кит Йейтс - Математика жизни и смерти. 7 математических принципов, формирующих нашу жизнь

В 2014 году, примерно в пиковый момент вспышки лихорадки Эбола, по результатам математического исследования был сделан вывод, что примерно 22 % новых случаев лихорадки Эбола вызваны контактами с трупами ее жертв [196]. В исследовании было высказано предположение, что базовый показатель репродукции вируса можно сократить до значений, при которых эпидемия утратит способность к самоподдерживающемуся росту. Для этого требовалось ограничить традиционные практики, включая погребальные обряды. Одной из наиболее важных мер, принятых властями стран Западной Африки и гуманитарными организациями, работавшими в этом районе, стал запрет на традиционные похоронные обряды и обеспечение безопасного и достойного захоронения всех жертв лихорадки. В сочетании с просветительскими кампаниями, рассказывающими об иных практиках, менее опасных, чем традиционные, и ограничениями на перемещение даже для здоровых, на первый взгляд, людей, вспышка лихорадки Эбола в итоге была купирована. 9 июня 2016 года, спустя почти два с половиной года после заражения Эмиля Уамуно, было объявлено о завершении вспышки лихорадки Эбола в Западной Африке.

Помимо активной помощи в борьбе с эпидемиями, математические модели эпидемий также могут объяснить необычные закономерности, свойственные различным заболеваниям. Так, ряд интересных вопросов сформировался вокруг детских болезней, таких как свинка и краснуха: почему их периодические вспышки поражают только детей? Возможно, предрасположенность к ним обусловлена каким-то до сих пор неизвестным свойством, присущим только детям? И почему эти болезни так долго сохраняются в нашем обществе? Может, они, словно в засаде, годами находятся в латентном состоянии, выбирая время для того, чтобы обрушиться на самых беззащитных?

Причина, по которой для детских заболеваний характерны периодические вспышки, заключается в том, что значение реального коэффициента репродукции с течением времени варьируется в зависимости от популяции восприимчивых к ним лиц. После того как крупная вспышка той же скарлатины поразит значительную часть незащищенной популяции детей, она не просто исчезает. Она сохраняется в популяции, но ее реальный коэффициент репродукции колеблется в районе единицы. Болезнь только поддерживает себя. Со временем население стареет, и рождаются новые, незащищенные дети. По мере роста незащищенной части популяции реальный коэффициент репродукции растет, что увеличивает вероятность новых вспышек. Когда болезнь наконец начинает распространяться, ее жертвы, как правило, принадлежат к незащищенному молодому поколению, поскольку большинство пожилых людей уже иммунизированы – ведь они столкнулись с этой болезнью раньше. Те же, кто не переболел скарлатиной в детстве, как правило, получают определенную степень защиты от нее, поскольку они меньше общаются с представителями инфицированной возрастной группы.

Концепция, что большое количество людей с иммунитетом может замедлить или даже остановить распространение инфекции, как это происходит в периоды покоя между вспышками детских болезней, на математическом языке называется популяционным иммунитетом [197]. Как ни странно, для работы этому эффекту общества не нужно, чтобы от заболевания были защищены все. Опустив значение реального коэффициента репродукции ниже единицы, можно разорвать цепь передачи инфекции и остановить распространение болезни. Популяционный иммунитет предполагает, что обеспеченная вакцинацией защита в некоторой мере распространяется и на тех, у кого иммунная система слишком слаба, чтобы переносить прививки (включая пожилых, новорожденных, беременных женщин и людей с ВИЧ). Это исключительно важно. Пороговое значение величины иммунной части населения, необходимое для защиты его восприимчивой части, варьируется в зависимости от того, насколько заболевание заразно. Ключом к тому, насколько эта доля велика, является базовый показатель репродукции R 0.

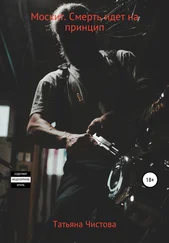
Рис. 24. Один инфицированный (черный круг) сталкивается с 20 восприимчивыми (белый круг) или вакцинированными (серый круг) лицами в течение недельного инфекционного периода. Если не вакцинирован никто (слева), один заразившийся заражает четырех других, т. е. базовый показатель репродукции R 0равен 4. При вакцинировании половины населения (в середине) заражаются только двое восприимчивых. Реальный коэффициент репродукции, R e, уменьшается до 2. Наконец, когда вакцинировано 3/4 населения (справа), в среднем заражается только один человек. Реальный коэффициент репродукции снижается до критического значения 1