Кит Йейтс - Математика жизни и смерти. 7 математических принципов, формирующих нашу жизнь

Памятуя об этих расходах, а также о гиперреакции на угрозу эпидемии, группа математиков Лондонской школы гигиены и тропической медицины разработала простую математическую модель, учитывающую инкубационный период [193]. Принимая во внимание средний 12-дневный инкубационный период для лихорадки Эбола и шесть с половиной часов полета из Фритауна в Сьерра-Леоне в Лондон, математики подсчитали, что эти новые дорогостоящие меры выявления инфицированных могли бы выявить лишь около 7 % пассажиров – носителей вируса Эбола. Они предположили, что эти деньги, возможно, было бы лучше потратить на развивающийся гуманитарный кризис в Западной Африке, который нанес бы удар по источнику проблемы и, следовательно, снизил риск передачи вируса в Великобританию. Это наилучший пример математического вмешательства – простого, решительного и основанного на фактах. Вместо того чтобы строить догадки, насколько эффективными могут быть скрининговые меры, простое математическое описание ситуации в состоянии дать мощное представление о сути происходящего и направить политику в нужное русло.

Отслеживание маршрута передачи инфекции, использованное для идентификации Эмиля Уамуно как нулевого пациента лихорадки Эбола, – далеко не уникальный опыт. Болезнь распространялась из своего очага в Мелианду несколькими путями. Фактически на ранних стадиях болезни она реплицировалась экспоненциально по нескольким независимым каналам, подобно мемам или вирусным маркетинговым кампаниям, описанным в первой главе. Один человек заражал трех других, которые продолжали заражать следующих; те заражали еще больше людей – в результате происходила вспышка заболевания. Определить, разовьется эта вспышка в масштабную эпидемию или выдохнется и забудется, можно с помощью всего одного показателя, уникального для каждой вспышки, – базового показателя репродукции.

Давайте представим, что население на некой территории полностью восприимчиво к определенным болезням – как это было с коренными жителями Мезоамерики в 1500-х годах до прибытия конкистадоров. Среднее число лиц, инфицированных одним носителем болезни, воздействию которой они прежде не подвергались, известно как базовый показатель репродукции и часто обозначается R 0(произносится «R-ноль»). Если болезнь имеет R 0менее 1, то инфекция быстро сходит на нет, так как каждый инфицированный в среднем передает болезнь менее чем одному другому. Вспышка не становится самоподдерживающейся. Если R 0больше 1, то инфекция будет распространяться в геометрической прогрессии.

Возьмем, к примеру, такое заболевание, как атипичная пневмония (SARS), имеющее базовый показатель репродукции 2. Первый человек с этим заболеванием – нулевой пациент. Он заражает двоих, каждый из которых распространяет болезнь еще на двоих – и так далее. Как мы видели в первой главе, рис. 23 иллюстрирует экспоненциальный рост, характеризующий начальную фазу распространения инфекции. Если бы она распространялась таким образом и далее, то через десять поколений вниз по цепочке прогрессии заразилось бы более 1000 человек. Еще десять шагов – и число зараженных превысит миллион.

На практике, как и в случае с распространением вирусной идеи, расширением пирамидальной схемы, ростом колонии бактерий или распространением популяции, экспоненциальный рост, прогнозируемый на основе базового показателя репродукции, редко поддерживается более чем на несколько поколений. Вспышки в конечном итоге достигают пика, а затем идут на спад из-за того, что контакты между инфицированными и восприимчивыми к вирусу людьми становятся реже.

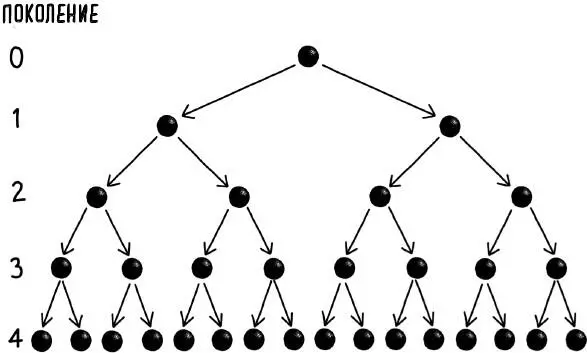
Рис. 23. Экспоненциальное распространение болезни с базовым показателем репродукции R 0равным 2. Первое инфицированное лицо считается нулевым поколением. К четвертому поколению инфицируются уже 16 человек

В конечном счете, даже когда зараженных не будет и вспышка официально закончится, некоторые восприимчивые к инфекции люди еще останутся. Еще в 1920-х годах Кермак и Маккендрик предложили формулу, в которой базовый показатель репродукции использовался для предсказания количества восприимчивых лиц, которых инфекция не затронет до самого конца вспышки. При значении R 0около 1,5 формула Кермака и Маккендрика предсказывает, что вспышка лихорадки Эбола в 2013–2016 годах поразила бы 58 % популяции, если бы не было принято никаких мер. Вспышки полиомиелита, напротив, имеют R 0около 6, что, по прогнозам Кермака и Маккендрика, означает, что без вмешательства только четверть процента населения переживет эпидемию, не заразившись.