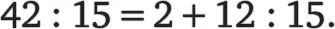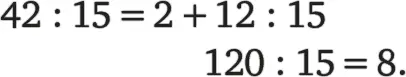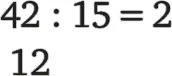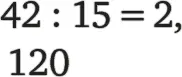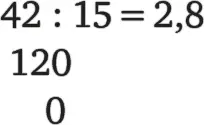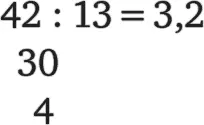Рудольф Ташнер - Число, пришедшее с холода. Когда математика становится приключением

0 0 3 0 0 3 0 0 3

и получает следующую строку:

1 4 4 5 9 5 6 5 6 5 8 9 7 9 3 2 3 8 4 6 2 6 4 3 3 8 3 2 7 9 5 0 2 8 8…

То есть отрезок отправленного сообщения будет выглядеть так:

1 4 4 5 9 5 6 5 6.

Смайли, однако, должен понимать, что Карла перехватит оба отправленных им шифрованных сообщения, и его люди напишут их одно под другим:

1 4 8 5 9 9 6 5 0

1 4 4 5 9 5 6 5 6.

Если теперь люди Карлы вычтут нижнее сообщение из верхнего по модулю десять, то получат

0 0 4 0 0 4 0 0 4,

то есть увидят явную систему, очевидный «узор». Обнаружение системы — это залог к успешной дешифровке вражеского кода. При многократном применении одного листка шифр становится очень ненадежным. Поэтому использовать листки блокнота можно только один раз, и блокнот называется «одноразовым».

Ситуация, при которой цифры бесконечно появляются друг за другом, известна уже школьникам начальных классов с момента, когда они начинают изучать деление. Это действие редко выполняется так же гладко, как при делении 42: 6 = 7. В большинстве случаев при делении получают остаток. Например, при делении 42 на 15 получают частное 2, потому что дважды пятнадцать целиком содержится в 42, но при этом получается остаток 12. Он получается, потому что дважды 15 не равно в точности 42, но лишь 30, и разница между 30 и 42 как раз и равна 12. Поэтому записывают:

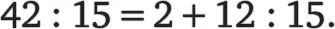
Однако деление остатка 12 на 15 невыполнимо, так как 15 ни одного раза не содержится в 12. Адам Ризе, научивший нас позиционной записи, смог выполнить деление дальше, воспользовавшись числом 0. Он добавил к 12 число 0, то есть умножил остаток 12 на 10, и смог таким образом довести деление до конца, разделив число 120 без остатка на 15. В двух строках это действие выглядит так:

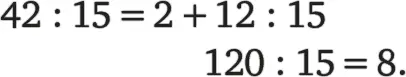
Результат он записывает в виде десятичного числа 2,8. Дети в школе учатся записывать обе эти строки так: сначала записывают деление 42 на 15 как

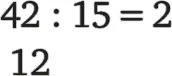
То есть аккуратно записывают остаток 12 под делимым 42. Затем к 12 «подвешивают» 0, а к частному 2 пририсовывают запятую:

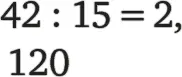
и делают следующий шаг: делят 120 на 15, получают число 8, которое записывают после запятой, а под числом 120 подписывают остаток 0:

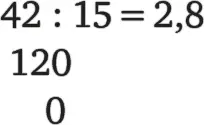
При делении 42 на 13 начало выглядит похоже:

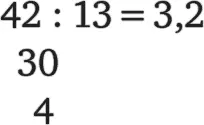
Однако в этом случае получается еще один остаток. В этом случае Адам Ризе предписывает нам снова приписать 0 к остатку и продолжить деление:

Снова получается остаток. Следовательно, надо продолжать процедуру дальше:

Конца этому процессу не видно. Но, во всяком случае, снова появился первый остаток — 3, значит, вся предыдущая процедура будет снова и снова повторяться до бесконечности. В результате мы получим «бесконечную десятичную дробь»

42: 13 = 3,230769230769230769230769230769230769230769…,

в которой последовательность цифр 230769 представляет собой так называемый период.

Ясно, что при делении целых чисел всегда получаются периодические бесконечные дроби, если деление не обрывают раньше, так как в каком-то месте должен получиться остаток, который уже получался в предыдущих делениях; существует лишь конечное число возможных остатков, а именно их число равно делителю.

Для знатоков предмета: число 10 должно быть так называемым «первообразным» корнем такого делителя. Другими словами: если обозначить делитель буквой m и делить ряд степеней 10, то лишь при делении числа 10 m — 1 на число m получается остаток 1. Например, число 10 является первообразным корнем делителей 7 или 113, но не является первообразным корнем делителя 3 (уже 10: 3 дает остаток 1) или делителя 13 (13 × 76923 = = 999 999, то есть уже при делении 10 6 на 13 получается остаток 1).

Если повезет, то может случиться так, что намного меньшее число, выступающее в роли делителя, приведет к этой чрезвычайно длинной и, как представляется, случайной последовательности — в лучшем случае числа, состоящего «только» из пары сотен разрядов. Конечно, это намного меньше числа, состоящего из 10 200 девяток, то есть из 10 200 разрядов. Однако 10 должно быть первообразным корнем этого приблизительно двухсотзначного делителя.