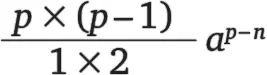Рудольф Ташнер - Число, пришедшее с холода. Когда математика становится приключением

( a + 1) p = ( a + 1) ( a + 1) ( a + 1)… ( a + 1) = a p + 1 + …

То, что здесь стыдливо обозначено точками …, — это все остальное, что получается от перемножения друг на друга всех слагаемых. В ходе такого перемножения будут получаться степени a p — 1, a p — 2, a p — 3, и вопрос заключается в том, насколько часто будет встречаться каждая из этих степеней. Например, степень a p — 1 получается оттого, что p — 1 первых слагаемых a перемножают с одним из всех вторых слагаемых 1. Всего возможностей для такого перемножения существует ровно p . Таким образом, степень a p — 1 появится на месте точек в виде pa p — 1. Или степень a p — 2 появляется в результате того, что p — 2 первых слагаемых a перемножаются с двумя вторыми слагаемыми. Сколько раз эта степень встретится в результатах перемножения? Для одного из обоих вторых слагаемых 1 существует p возможностей выбора, а для другого второго слагаемого таких возможностей остается уже p — 1. Всего таких возможностей, следовательно, будет p × ( p — 1). Однако это выражение надо разделить на произведение 1 × 2, потому что совершенно несущественно, какое из двух слагаемых 1 было выбрано первым, а какое — вторым. Таким образом, степень a p — 2встречается среди слагаемых, замененных точками,

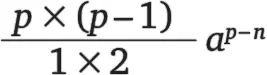
раз. В общем виде можно представить, что степень a p — n возникает в результате того, что p — n первых слагаемых a перемножают в точности с n вторых слагаемых 1. Сколько раз встретится в окончательном результате перемножения степень a p — n ? Для первого из n вторых слагаемых существует ровно p возможных выборов, для второго слагаемого 1 существует только p – 1 возможных выборов, и так далее, вплоть до n -го слагаемого 1, для которого число возможных выборов равно p — n + 1. В результате число возможных выборов становится равно p × ( p — 1) × … × ( p – n + 1). Это число, однако, надо разделить на произведение 1 × 2 × 3 × … × n , ибо какое из n слагаемых 1 будет выбрано в качестве первого, второго, …, n -го, представляется несущественным. Таким образом, степень a p — n встретится на месте точек

раз.

Множители перед степенями a выглядят дробями только по видимости; на самом деле это целые числа. Другими словами, знаменатель записанной дроби наверняка является делителем числителя. Тем не менее простое число p , записанное первым, не делится на знаменатель, так как именно в этом и заключается суть простого числа. Поэтому множители, стоящие перед степенями a , начиная с a p — 1и заканчивая a = a 1, являются не только целыми числами, но и числами, кратными простому числу p .

Обобщая, получаем:

( a + 1) p = a p + 1 + …,

причем все числа, скрытые за обозначением …, делятся на простое число p .

Допустим, утверждает далее Ферма, что мы уже знаем, что a p — a без остатка делится на p . Тогда, согласно уравнению

( a + 1) p –( a + 1) = a p + 1 + … — ( a + 1) = a p + 1 + … – a — 1 = a p — a + …

и вследствие того факта, что все числа, скрытые за многоточием, делятся на p , разность ( a + 1) p — ( a + 1) тоже делится на p .

Тем самым Ферма наглядно показал то, что хотел доказать, ибо 1 p — 1, очевидно, делится на p . Проведенное выше рассуждение показывает, что отсюда и 2 p — 2 тоже делится на p . Точно такое же рассуждение доказывает, что и 3 p — 3 тоже делится на p . Точно такое же рассуждение, проведенное еще раз, доказывает, что и 4 p — 4 делится на p . Так можно от каждого числа a , о котором известно, что a p — a делится на p , перейти к следующему числу a + 1 и уже относительно его установить, что ( a + 1) p — ( a + 1) делится без остатка на p .