Макс Тегмарк - Life 3.0 - Being Human in the Age of Artificial Intelligence

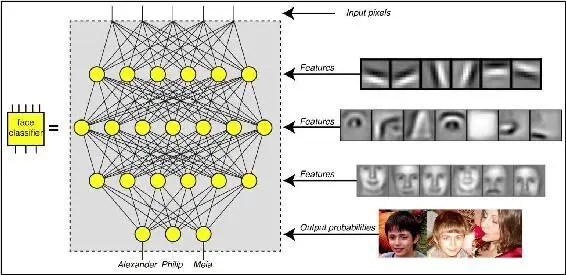
Figure 2.9: A network of neurons can compute functions just as a network of NAND gates can. For example, artificial neural networks have been trained to input numbers representing the brightness of different image pixels and output numbers representing the probability that the image depicts various people. Here each artificial neuron (circle) computes a weighted sum of the numbers sent to it via connections (lines) from above, applies a simple function and passes the result downward, each subsequent layer computing higher-level features. Typical face-recognition networks contain hundreds of thousands of neurons; the figure shows merely a handful for clarity.

The success of these simple artificial neural networks is yet another example of substrate independence: neural networks have great computational power seemingly independent of the low-level nitty-gritty details of their construction. Indeed, George Cybenko, Kurt Hornik, Maxwell Stinchcombe and Halbert White proved something remarkable in 1989: such simple neural networks are universal in the sense that they can compute any function arbitrarily accurately, by simply adjusting those synapse strength numbers accordingly. In other words, evolution probably didn’t make our biological neurons so complicated because it was necessary, but because it was more efficient—and because evolution, as opposed to human engineers, doesn’t reward designs that are simple and easy to understand.

When I first learned about this, I was mystified by how something so simple could compute something arbitrarily complicated. For example, how can you compute even something as simple as multiplication, when all you’re allowed to do is compute weighted sums and apply a single fixed function? In case you’d like a taste of how this works, figure 2.10 shows how a mere five neurons can multiply two arbitrary numbers together, and how a single neuron can multiply three bits together.

Although you can prove that you can compute anything in theory with an arbitrarily large neural network, the proof doesn’t say anything about whether you can do so in practice, with a network of reasonable size. In fact, the more I thought about it, the more puzzled I became that neural networks worked so well.

For example, suppose that we wish to classify megapixel grayscale images into two categories, say cats or dogs. If each of the million pixels can take one of, say, 256 values, then there are 256 1000000possible images, and for each one, we wish to compute the probability that it depicts a cat. This means that an arbitrary function that inputs a picture and outputs a probability is defined by a list of 256 1000000probabilities, that is, way more numbers than there are atoms in our Universe (about 10 78). Yet neural networks with merely thousands or millions of parameters somehow manage to perform such classification tasks quite well. How can successful neural networks be “cheap,” in the sense of requiring so few parameters? After all, you can prove that a neural network small enough to fit inside our Universe will epically fail to approximate almost all functions, succeeding merely on a ridiculously tiny fraction of all computational tasks that you might assign to it.

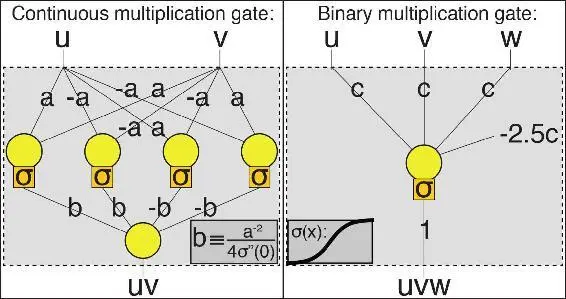
Figure 2.10: How matter can multiply, but using not NAND gates as in figure 2.7 but neurons. The key point doesn’t require following the details, and is that not only can neurons (artificial or biological) do math, but multiplication requires many fewer neurons than NAND gates. Optional details for hard-core math fans: Circles perform summation, squares apply the function σ , and lines multiply by the constants labeling them. The inputs are real numbers (left) and bits (right). The multiplication becomes arbitrarily accurate as a → 0 (left) and c → ∞ (right). The left network works for any function σ ( x ) that’s curved at the origin (with second derivative σ ″ (0) ≠ 0), which can be proven by Taylor expanding σ ( x ). The right network requires that the function σ ( x ) approaches 0 and 1 when x gets very small and very large, respectively, which is seen by noting that uvw = 1 only if u + v + w = 3. (These examples are from a paper I wrote with my students Henry Lin and David Rolnick, “Why Does Deep and Cheap Learning Work So Well?,” which can be found at http://arxiv.org/abs/1608.08225.) By combining together lots of multiplications (as above) and additions, you can compute any polynomials, which are well known to be able to approximate any smooth function.

I’ve had lots of fun puzzling over this and related mysteries with my student Henry Lin. One of the things I feel most grateful for in life is the opportunity to collaborate with amazing students, and Henry is one of them. When he first walked into my office to ask whether I was interested in working with him, I thought to myself that it would be more appropriate for me to ask whether he was interested in working with me: this modest, friendly and bright-eyed kid from Shreveport, Louisiana, had already written eight scientific papers, won a Forbes 30-Under-30 award, and given a TED talk with over a million views—and he was only twenty! A year later, we wrote a paper together with a surprising conclusion: the question of why neural networks work so well can’t be answered with mathematics alone, because part of the answer lies in physics. We found that the class of functions that the laws of physics throw at us and make us interested in computing is also a remarkably tiny class because, for reasons that we still don’t fully understand, the laws of physics are remarkably simple. Moreover, the tiny fraction of functions that neural networks can compute is very similar to the tiny fraction that physics makes us interested in! We also extended previous work showing that deep-learning neural networks (they’re called “deep” if they contain many layers) are much more efficient than shallow ones for many of these functions of interest. For example, together with another amazing MIT student, David Rolnick, we showed that the simple task of multiplying n numbers requires a whopping 2 n neurons for a network with only one layer, but takes only about 4 n neurons in a deep network. This helps explain not only why neural networks are now all the rage among AI researchers, but also why we evolved neural networks in our brains: if we evolved brains to predict the future, then it makes sense that we’d evolve a computational architecture that’s good at precisely those computational problems that matter in the physical world.

Now that we’ve explored how neural networks work and compute, let’s return to the question of how they can learn. Specifically, how can a neural network get better at computing by updating its synapses?

In his seminal 1949 book, The Organization of Behavior: A Neuropsychological Theory, the Canadian psychologist Donald Hebb argued that if two nearby neurons were frequently active (“firing”) at the same time, their synaptic coupling would strengthen so that they learned to help trigger each other—an idea captured by the popular slogan “Fire together, wire together.” Although the details of how actual brains learn are still far from understood, and research has shown that the answers are in many cases much more complicated, it’s also been shown that even this simple learning rule (known as Hebbian learning) allows neural networks to learn interesting things. John Hopfield showed that Hebbian learning allowed his oversimplified artificial neural network to store lots of complex memories by simply being exposed to them repeatedly. Such exposure to information to learn from is usually called “training” when referring to artificial neural networks (or to animals or people being taught skills), although “studying,” “education” or “experience” might be just as apt. The artificial neural networks powering today’s AI systems tend to replace Hebbian learning with more sophisticated learning rules with nerdy names such as “backpropagation” and “stochastic gradient descent,” but the basic idea is the same: there’s some simple deterministic rule, akin to a law of physics, by which the synapses get updated over time. As if by magic, this simple rule can make the neural network learn remarkably complex computations if training is performed with large amounts of data. We don’t yet know precisely what learning rules our brains use, but whatever the answer may be, there’s no indication that they violate the laws of physics.