Макс Тегмарк - Life 3.0 - Being Human in the Age of Artificial Intelligence

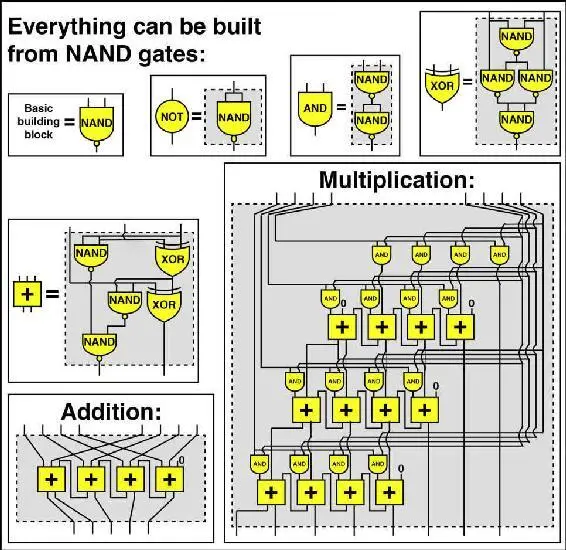
Figure 2.7: Any well-defined computation can be performed by cleverly combining nothing but NAND gates. For example, the addition and multiplication modules above both input two binary numbers represented by 4 bits, and output a binary number represented by 5 bits and 8 bits, respectively. The smaller modules NOT, AND, XOR and + (which sums three separate bits into a 2-bit binary number) are in turn built out of NAND gates. Fully understanding this figure is extremely challenging and totally unnecessary for following the rest of this book; I’m including it here just to illustrate the idea of universality—and to satisfy my inner geek.

This fact that exactly the same computation can be performed on any universal computer means that computation is substrate-independent in the same way that information is: it can take on a life of its own, independent of its physical substrate! So if you’re a conscious superintelligent character in a future computer game, you’d have no way of knowing whether you ran on a Windows desktop, a Mac OS laptop or an Android phone, because you would be substrate-independent. You’d also have no way of knowing what type of transistors the microprocessor was using.

I first came to appreciate this crucial idea of substrate independence because there are many beautiful examples of it in physics. Waves, for instance: they have properties such as speed, wavelength and frequency, and we physicists can study the equations they obey without even needing to know what particular substance they’re waves in. When you hear something, you’re detecting sound waves caused by molecules bouncing around in the mixture of gases that we call air, and we can calculate all sorts of interesting things about these waves—how their intensity fades as the square of the distance, such as how they bend when they pass through open doors and how they bounce off of walls and cause echoes—without knowing what air is made of. In fact, we don’t even need to know that it’s made of molecules: we can ignore all details about oxygen, nitrogen, carbon dioxide, etc., because the only property of the wave’s substrate that matters and enters into the famous wave equation is a single number that we can measure: the wave speed, which in this case is about 300 meters per second. Indeed, this wave equation that I taught my MIT students about in a course last spring was first discovered and put to great use long before physicists had even established that atoms and molecules existed!

This wave example illustrates three important points. First, substrate independence doesn’t mean that a substrate is unnecessary, but that most of its details don’t matter. You obviously can’t have sound waves in a gas if there’s no gas, but any gas whatsoever will suffice. Similarly, you obviously can’t have computation without matter, but any matter will do as long as it can be arranged into NAND gates, connected neurons or some other building block enabling universal computation. Second, the substrate-independent phenomenon takes on a life of its own, independent of its substrate. A wave can travel across a lake, even though none of its water molecules do—they mostly bob up and down, like fans doing “the wave” in a sports stadium. Third, it’s often only the substrate-independent aspect that we’re interested in: a surfer usually cares more about the position and height of a wave than about its detailed molecular composition. We saw how this was true for information, and it’s true for computation too: if two programmers are jointly hunting a bug in their code, they’re probably not discussing transistors.

We’ve now arrived at an answer to our opening question about how tangible physical stuff can give rise to something that feels as intangible, abstract and ethereal as intelligence: it feels so non-physical because it’s substrate-independent, taking on a life of its own that doesn’t depend on or reflect the physical details. In short, computation is a pattern in the spacetime arrangement of particles, and it’s not the particles but the pattern that really matters! Matter doesn’t matter.

In other words, the hardware is the matter and the software is the pattern. This substrate independence of computation implies that AI is possible: intelligence doesn’t require flesh, blood or carbon atoms.

Because of this substrate independence, shrewd engineers have been able to repeatedly replace the technologies inside our computers with dramatically better ones, without changing the software. The results have been every bit as spectacular as those for memory devices. As illustrated in figure 2.8, computation keeps getting half as expensive roughly every couple of years, and this trend has now persisted for over a century, cutting the computer cost a whopping million million million (10 18) times since my grandmothers were born. If everything got a million million million times cheaper, then a hundredth of a cent would enable you to buy all goods and services produced on Earth this year. This dramatic drop in costs is of course a key reason why computation is everywhere these days, having spread from the building-sized computing facilities of yesteryear into our homes, cars and pockets—and even turning up in unexpected places such as sneakers.

Why does our technology keep doubling its power at regular intervals, displaying what mathematicians call exponential growth? Indeed, why is it happening not only in terms of transistor miniaturization (a trend known as Moore’s law ), but also more broadly for computation as a whole (figure 2.8), for memory (figure 2.4) and for a plethora of other technologies ranging from genome sequencing to brain imaging? Ray Kurzweil calls this persistent doubling phenomenon “the law of accelerating returns.”

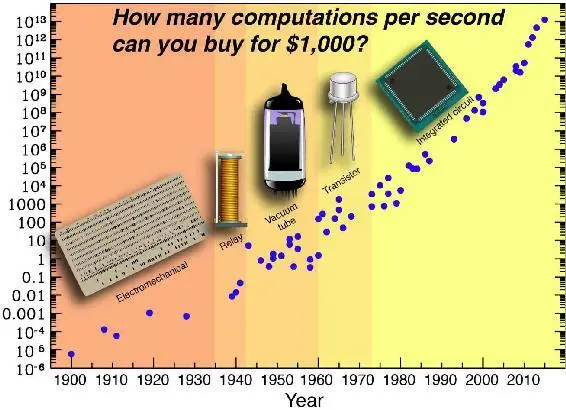
Figure 2.8: Since 1900, computation has gotten twice as cheap roughly every couple of years. The plot shows the computing power measured in floating-point operations per second (FLOPS) that can be purchased for $1,000.3 The particular computation that defines a floating point operation corresponds to about 10 5elementary logical operations such as bit flips or NAND evaluations.

All examples of persistent doubling that I know of in nature have the same fundamental cause, and this technological one is no exception: each step creates the next. For example, you yourself underwent exponential growth right after your conception: each of your cells divided and gave rise to two cells roughly daily, causing your total number of cells to increase day by day as 1, 2, 4, 8, 16 and so on. According to the most popular scientific theory of our cosmic origins, known as inflation, our baby Universe once grew exponentially just like you did, repeatedly doubling its size at regular intervals until a speck much smaller and lighter than an atom had grown more massive than all the galaxies we’ve ever seen with our telescopes. Again, the cause was a process whereby each doubling step caused the next. This is how technology progresses as well: once technology gets twice as powerful, it can often be used to design and build technology that’s twice as powerful in turn, triggering repeated capability doubling in the spirit of Moore’s law.

Something that occurs just as regularly as the doubling of our technological power is the appearance of claims that the doubling is ending. Yes, Moore’s law will of course end, meaning that there’s a physical limit to how small transistors can be made. But some people mistakenly assume that Moore’s law is synonymous with the persistent doubling of our technological power. Contrariwise, Ray Kurzweil points out that Moore’s law involves not the first but the fifth technological paradigm to bring exponential growth in computing, as illustrated in figure 2.8: whenever one technology stopped improving, we replaced it with an even better one. When we could no longer keep shrinking our vacuum tubes, we replaced them with transistors and then integrated circuits, where electrons move around in two dimensions. When this technology reaches its limits, there are many other alternatives we can try—for example, using three-dimensional circuits and using something other than electrons to do our bidding.