Андрей Павлов - Геометрия - Планиметрия в тезисах и решениях. 9 класс

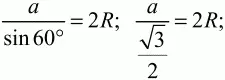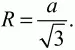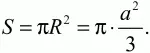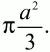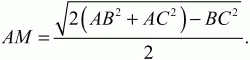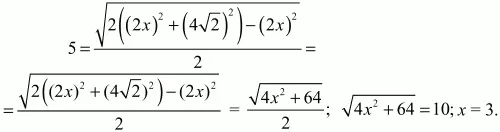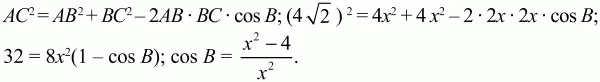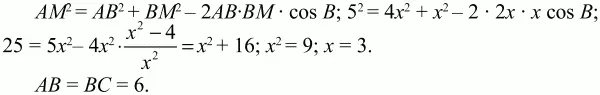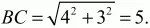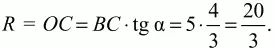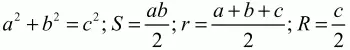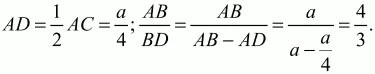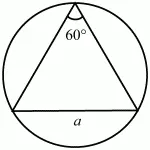
Рис. 135.

Решение. Обозначим сторону треугольника через а. Тогда по теореме синусов имеем:

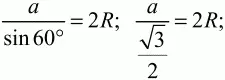
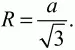
Площадь круга:

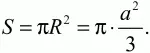
Ответ:

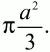
20. Основание равнобедренного треугольника равно 4?2, медиана боковой стороны равна 5. Найдите длину боковой стороны (рис. 136). (2)

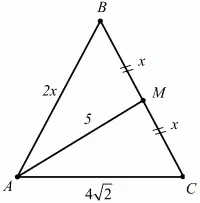
Рис. 136.

Решение. Можно воспользоваться готовой формулой длины медианы:

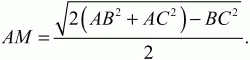
Обозначим АВ через 2х, тотда ВМ = МС = х (см. рис.).

Имеем:

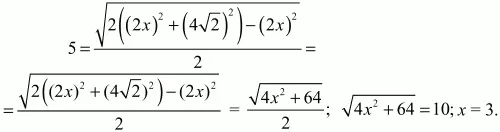
АВ = ВС = 6.

Задачу можно решить по-другому. Из ?ABC по теореме косинусов:

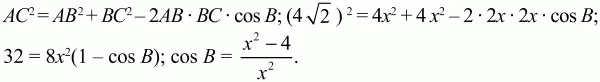
Далее, по той же теореме косинусов из ?АМВ:

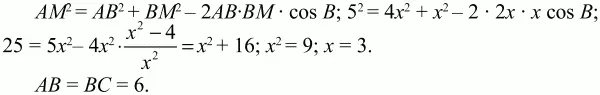
Ответ: 6.

21. На основании равнобедренного треугольника, равном 8 см, как на хорде, построена окружность, касающаяся боковых сторон треугольника. Найдите радиус окружности, если длина высоты, опущенной на основание треугольника, равна 3 см (рис. 137). (2)

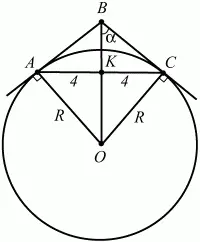
Рис. 137.

Решение. Пусть данный треугольник ABC, где АВ = ВС; ВК = 3; АК = КС = 4 (см. рис.). Угол ОВС обозначим через ?. Из треугольника ВКС по теореме Пифагора находим:

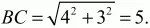
Из того же треугольника следует: tg ? = 4/3. Радиус окружности R = ОС найдём из треугольника ВСО:

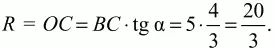
Ответ: 20/3 см.

22. В равнобедренном треугольнике боковая сторона равна 12, а угол при вершине – 120°. Определите высоту треугольника. (1)

23. В равнобедренном треугольнике основание и опущенная на него высота равны 4. Найдите площадь описанного круга. (1)

24. В равнобедренном треугольнике высота равна 8, а основание относится к боковой стороне, как 6:5. Найдите радиус вписанной окружности. (1)

25. Длина окружности, описанной около равностороннего треугольника, равна 4. Найдите площадь заштрихованного сектора (рис. 138). (2)

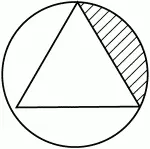
Рис. 138.

26. Докажите, что сумма расстояний от любой точки равностороннего треугольника до его сторон равна длине высоты треугольника. (2)

Для прямоугольного треугольника с катетами а, b и гипотенузой с, помимо общих формул (см. п. 1.1 этой главы), характерны следующие соотношения:

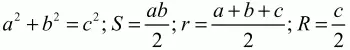
(центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы); а = csin ? = ccos ? = btg? = bctg?.

27. В прямоугольном треугольнике ABC, где угол АСВ = 90°, проведена высота CD. Известно, что угол СВА = 30°.

Найдите АВ/BD (рис. 139). (1)

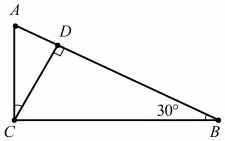
Рис. 139.

Решение. Пусть АВ = а; тогда из ?ABC получаем: АС = a/2 (катет, лежащий напротив угла в 30°, равен половине гипотенузы). Далее, ?ACD = ?СВА = 30°, так как эти углы имеют взаимноперпендикулярные стороны. Из ?ACD следует:

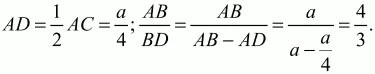
Ответ: 4/3.

28. Периметр прямоугольного треугольника равен 24 см, а его площадь равна 24 см2. Найдите площадь описанного около треугольника круга (рис. 140). (2)