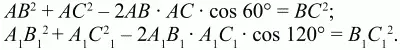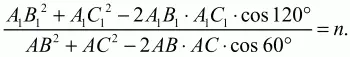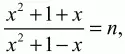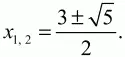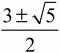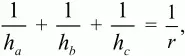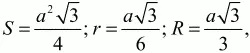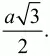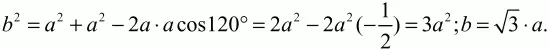Андрей Павлов - Геометрия - Планиметрия в тезисах и решениях. 9 класс

9. В треугольниках ABC и A1B1C1 длина стороны АВ равна длине стороны А1В1, длина стороны АС равна длине стороны А1С1, величина угла ВАС равна 60° и величина угла В1А1С1 равна 120°. Известно, что отношение длины В1С1 к длине ВС равно ?n (где n – целое число). Найти отношение длины АВ к длине АС. При каких значениях n задача имеет хотя бы одно решение (рис. 133)? (3)

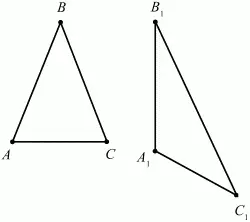
Рис. 133.

Решение: Пусть ABC и A1B1C1 – данные в условии задачи треугольники. Применяя теорему косинусов к треугольникам ABC и А1В1С1, имеем:

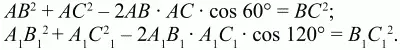
Т. к. по условию задачи В1С1 :ВС = ?n, то

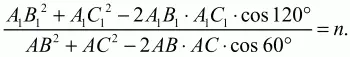
Поскольку А1В1 = АВ и А1С1 = АС, то, разделив числитель и знаменатель дроби в левой части равенства (1) на АС2и обозначив АВ: АС через х, получим равенство:

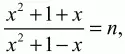
откуда ясно, что искомое отношение длины АВ к длине АС есть корень уравнения

х2(n – 1) – х(n + 1) + n – 1 = 0. (2)

Т. к. В1С1 > ВС, то n > 1. Следовательно, уравнение (2) является квадратным. Его дискриминант равен (n + 1)2– 4(n – 1)2= – 3n2+ 10n – 3.

Уравнение (2) будет иметь решения, если – 3n2+ 10n – 3 ? 0, т. е. при -1/3 ? n ? 3. Т. к. n – натуральное число, большее 1, то уравнение (2) имеет решения при n = 2 и n = 3. При n = 3 уравнение (2) имеет корень х = 1; при n = 2 уравнение имеет корни

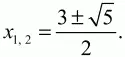
Ответ: отношение длины АВ к длине АС равно

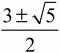
при n = 2; равно 1 при n = 3; при остальных n решений нет.

10. В треугольнике ABC высота AD на 4 см меньше стороны ВС. Сторона АС равна 5 см. Найдите периметр треугольника ABC, если его площадь равна 16 см2. (1)

11. Докажите, что для любого треугольника выполняется равенство:

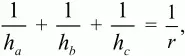
где ha, hb и hc – высоты треугольника, а r – радиус вписанной окружности. (2)

12. Основание треугольника равно ?2. Найдите длину отрезка прямой, параллельной основанию и делящей площадь треугольника пополам.(2)

13. Найдите площадь треугольника по стороне а и прилежащим к ней углам ? и ?. (2)

14. В треугольнике ABC длина высоты BD равна 6 см, длина медианы СЕ равна 5 см, расстояние от точки пересечения отрезков BD и СЕ до стороны АС равно 1 см. Найти длину стороны АВ. (3)

15. В треугольнике ABC высота BD равна 11,2, а высота АЕ равна 12. Точка Е лежит на стороне ВС, и BE: ЕС = 5:9. Найти длину стороны АС. (3)

16. В треугольнике ABC длина стороны АС равна 3, ?ВАС = ?/6 и радиус описанной окружности равен 2. Доказать, что площадь треугольника ABC меньше 3. (3)

17. В треугольнике ABC медианы, проведенные к сторонам АС и ВС, пересекаются под прямым углом. Длина стороны АС равна b, длина стороны ВС равна а. Найти длину стороны АВ. (3)

К задачам на равнобедренный треугольник применимы все формулы п. 1.1 этой главы, разве что во всех формулах b = с, ? = ?.

В случае равностороннего треугольника формулы значительно упрощаются, т. к. а = b = с, ? = ? = ? = 60°. Тогда

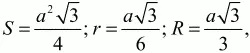
длины всех медиан, высот и биссектрис равны

18. Один из углов равнобедренного треугольника равен 120°. Найдите отношение сторон треугольника (рис. 134). (1)

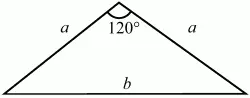
Рис. 134.

Решение. Обозначим основание треугольника через b, боковые стороны через а (см. рис.). По теореме косинусов

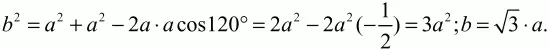
Тогда отношения сторон треугольника а: а: в = 1:1:?3.

Ответ: 1:1:?3.

19. Найдите площадь круга, описанного вокруг равностороннего треугольника со стороной а (рис. 135). (1)