Микель Альберти - Мир математики. т 40. Математическая планета. Путешествие вокруг света

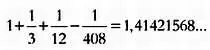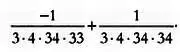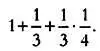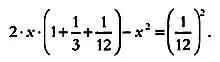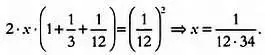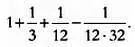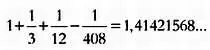
Позднее, в XV веке, к этому числу были добавлены еще два члена, и в результате оно стало равняться корню из 2 с точностью до семи знаков:

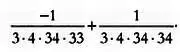
Откуда взялись эти цифры и число 34, в Шульба-Сутрах ничего не сказано. В них, как и во многих других математических текстах, зафиксированы лишь ответы, а не пути к решениям. Существует гипотеза, согласно которой индийский алгоритм вычисления корня из 2 основан на методе, известном еще вавилонянам. Мы уже показали, что им удалось с удивительной точностью вычислить длину диагонали квадрата, но нам ничего не известно о том, какой метод они при этом использовали и был он алгебраическим или геометрическим.

Как математики воссоздают творческий процесс решения задачи? Нужно провести некий воображаемый путь, выбрав в качестве начала точку, к которой пришел тот, кто решил задачу. Если мы узнаем, о чем думал автор решения, зафиксированного в Шульба-Сутрах, указанные дроби и числа обретут смысл.

Среди наиболее вероятных объяснений — теория индийского математика Датты, жившего в первой трети XX века. Начнем с того, что приближенное значение корня из 2 получается при помощи числовой последовательности, которая начинается с единицы (такова длина стороны квадрата):

{1, 1,33333, 1,41467, 1,4142157, 1,4142135 } — > √2.

Длина стороны квадрата и его площадь равны единице. Так как на первом шаге мы прибавляем к единице одну треть, разделим квадрат на три равные части. Получим три прямоугольника. Обозначим два первых прямоугольника через А и В и разделим третий прямоугольник на три равные части. Каждая из этих частей будет представлять собой квадрат. Обозначим верхний квадрат через С и разделим два нижних на четыре части каждый. Получим рисунок.

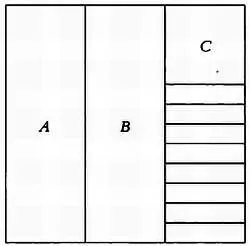
Имеем одиннадцать фигур ( А, В, С и восемь маленьких прямоугольников). Расположим их вокруг исходного квадрата следующим образом.

Заполнив пустой угол, получим новый квадрат. Его площадь будет больше площади искомого удвоенного квадрата на величину площади этого пустого угла, так как площадь добавленных фигур равна исходному квадрату. Заметим, что если мы добавим к этой фигуре небольшой квадрат в углу, то площадь полученного квадрата будет в точности совпадать с той, что указана в Шульба-Сутрах:

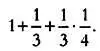
Датта объясняет использование дроби 1/(3·4·34) с алгебраической точки зрения, свойственной скорее западной математике. По его мнению, пустой угол фигуры — это излишек, который распределяется между двумя ограничивающими его сторонами. Иными словами, этот пустой угол (его площадь равна 1/12 2) делится на два прямоугольника и новый пустой угол со стороной х , которые мы «отрежем» от верхней и правой боковой стороны фигуры:

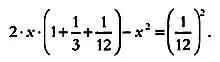
Далее Датта заключает, что площадь нового пустого угла, квадратика со стороной х , пренебрежимо мала, и выполняется соотношение:

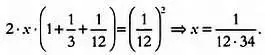
Возможно, именно так рассуждал индийский автор Шульба-Сутр, однако приведенные алгебраические методы и пренебрежение малыми величинами кажутся не слишком уместными при поиске все более точных значений. Чтобы поставить себя на место индийского автора и понять ход его рассуждений, нужно найти геометрическое обоснование этого необычного знаменателя, то есть числа 34. Разделим квадратный пустой угол со стороной 1/12 на столько частей, сколько раз этот квадрат укладывается на верхней и правой сторонах фигуры, то есть на 16 + 16 = 32 части. Отсечем от каждого из 16 квадратиков, расположенных вдоль стороны фигуры, полосу шириной 1/(12·32) и получим новый многоугольник, вписанный в квадрат. Длина стороны этого многоугольника будет равна:

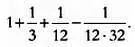
Площадь этого квадрата намного ближе к искомому значению: