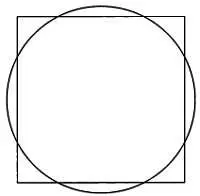
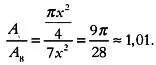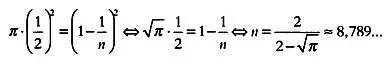С точки зрения современного человека площади этих фигур действительно схожи:
S 8 = π· 4,5 2= 63,617… кв. ед.
Их подобие нетрудно видеть на рисунке.
S квадрата = 8 2= 64 кв. ед.
Как считают Робинс и Шут, ответ на этот вопрос заключался в том, как диаметр окружности связывался со стороной квадрата. Если соединить вершину квадрата с серединой его стороны, получится прямоугольный треугольник с гипотенузой, равной √80. Это значение весьма схоже с диаметром окружности, равным √81 = 9.
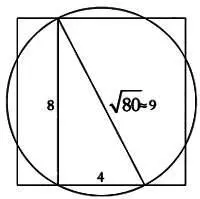
Любопытно, что если мы примем длину гипотенузы прямоугольного треугольника со сторонами 8 и 4 равной не √80, а 9, то получим еще более точное значение площади круга (64 ближе к 63,617, чем 62,83):
Неверная длина гипотенузы: 8 2= 64 кв. ед.
Точное значение: π· 4,5 2= 63,617… кв. ед.
Точная длина гипотенузы: π ·(√80/2) 2= 62,8318… кв. ед.
В любом случае ошибка будет меньше, если мы примем площадь круга диаметром 9 единиц равной 64 кв. ед., а не 63 кв. ед. (такова площадь неправильного восьмиугольника, рассмотренного ранее).
Неудивительно, что при решении этой задачи был выбран квадрат со стороной 9 единиц. Но почему именно 9? Если мы возьмем за основу квадрат со стороной в 3 единицы, то получим, что площадь восьмиугольника равна 7 кв. ед. Построить квадрат такой площади нельзя без использования иррациональных чисел. Площади квадратов со сторонами, например, 4 и 9 будут слишком далеки от реального значения. Возможно, для построения восьмиугольника египтяне брали за основу квадрат с длиной стороны, кратной 3. Но какое число, кратное 3, удобнее всего? Соотношение между площадью вписанного круга ( S о ), площадью квадрата со стороной 3 х и площадью вписанного неправильного восьмиугольника ( S 8 ) таково:
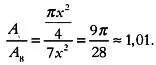
Чтобы построить квадрат, почти равный по площади восьмиугольнику, нужно найти число с такое, что с 2 = 7 х 2. Для целых с это уравнение не имеет решений, однако можно найти приближенное значение с примерно = x √7, например с = 8. Именно его использовали египтяне, получая очень близкие результаты: 7х 2= 63,с 2= 64.
Рей Пастор и Бабини считают, что египтяне вывели правило по результатам действий с дробными частями единицы. Так как требуется вычесть из диаметра его девятую часть, возникает вопрос: какую дробную часть диаметра вида 1/ n , где n — натуральное, необходимо рассмотреть, чтобы найти длину стороны эквивалентного квадрата? Пусть диаметр окружности D = 1. Вычтем из него дробь 1/ n и вычислим, каким должно быть значение n , чтобы при возведении этой разности в квадрат получалось число, близкое к площади круга с диаметром 1.
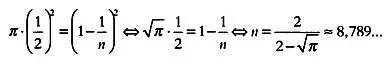
Математика с большой буквы
Значительная часть известной нам сегодня математики создана на основе традиций, заложенных Евклидом в его «Началах». Этот труд не просто сборник задач и решений. В нем описано математическое мышление, которое принималось за образец вплоть до середины XX века, пока Бертран Рассел не пошатнул сами его основы.
Критики «Начал» не согласны уже с первой строчкой трактата, где приводится определение точки как чего-то, что не имеет частей. Сегодня точка определяется как элемент аффинного, или топологического пространства. Рассмотрим подробнее критику первого предложения, в котором идет речь о построении равностороннего треугольника. Это предложение часто рассматривается как иллюстрация парадигмы метода Евклида: оно представляет собой формулировку теоремы, которая доказывается на основе приведенных ранее аксиом. В доказательстве раскрывается метод, при помощи которого древние египтяне, возможно, размечали на земле прямые углы оснований своих пирамид.
В предложении 1 описывается построение равностороннего треугольника на данном отрезке. Пусть дан отрезок АВ . Нужно построить с помощью циркуля окружность радиуса АВ с центром в точке А . Далее аналогично строится окружность с центром в точке В . Две построенные окружности пересекутся в точках Р и Q . Эти точки будут находиться на одинаковом расстоянии от А и В . Следовательно, треугольники АВР и ABQ равносторонние.
Читать дальше