Микель Альберти - Мир математики. т 40. Математическая планета. Путешествие вокруг света

Фигурам, изображенным в верхней правой ячейке глиняной таблички, соответствуют числа в третьем столбце таблицы. Под этими фигурами на табличке изображены три маленьких конуса, обозначающие остаток от деления (им соответствует четвертый столбец таблицы). Разумеется, деление было проведено по всем правилам.

Древние египтяне, жившие в 2000 году до н. э., с легкостью выполняли умножение и деление на 10 — для этого им было достаточно заменить символы, обозначавшие цифры исходного числа, меньшими или большими символами соответственно.

На следующем рисунке в качестве примера показано, как записывались числа 48 и 480 (напомним, что египтяне писали справа налево).

При умножении на другие величины они использовали не алгоритм, подобный нашему, а последовательное умножение или деление на 2. Так, чтобы умножить 117 на 14, они записывали числа в два столбца. В левом столбце записывались последовательные степени двойки, в правом — числа, кратные 14. Запись прекращалась, когда следующая степень двойки превышала число, на которое умножалось 14, то есть 117.

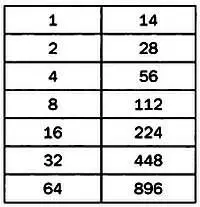
Теперь нужно выбрать из правого столбца числа, которые в сумме дают 117:

1 + 4 + 16 + 32 + 64 = 117.

Следовательно, результат умножения равен сумме чисел из правого столбца, соответствующих этим слагаемым:

14 + 36 + 224 + 448 + 896 = 1638.

Действия, выполняемые в левой колонке, равносильны представлению большего из множителей в двоичной системе счисления:

117 = 1·2 6+ 1·2 5+ 1·2 4+ 0·2 3+ 1·2 2+ 0·2 1+ 1·2 0= 1110 101 (в двоичной системе)

Это выражение определяет результат. Египтяне, жившие 4 тысячи лет назад, при умножении, по-видимому, неосознанно переводили числа в другую систему счисления. Их метод оказался успешным потому, что из левого столбца всегда можно выбрать числа таким образом, что их сумма будет равна требуемому числу. Иными словами, натуральное число всегда можно выразить в двоичной системе счисления.

Рассмотрим несколько примеров, показывающих, почему это так:

12 = 2 2·3 = 2 2·(2 + 1) = 2 3 + 2 2.

15 = 3·5 = (2 + 1)·(2 2+ 1) = 2 3·2 2+ 2 + 1.

Первые натуральные числа также обладают этим свойством:

1 = 2 0, 2 = 2 1, 3 = 2 1+ 2 0, 4 = 2 2, 5 = 2 2 + 1, 6 = 2 2+ 2 1, 7 = 2 2+ 2 1+ 2 0…

Если п — натуральное число, обладающее этим свойством, то следующее за ним число, n + 1, также будет обладать этим свойством. В самом деле, если n четное, то ни одно из составляющих его слагаемых не будет равно 2 0= 1. Следовательно, именно эту степень двойки нужно будет добавить к n , чтобы получить следующее число, n + 1. Таким образом, n + 1 будет суммой степеней двойки. Если же n нечетное, то его разложение на сумму степеней двойки будет оканчиваться 2 0. Чтобы получить из n следующее число, n + 1, к нему нужно будет добавить единицу, то есть 2 0. Но в разложении этого числа уже есть одна единица, поэтому получим 2 0+ 2 0= 1 + 1 = 2 = 2 1. Если слагаемое 2 1уже фигурировало в разложении, мы получим новое слагаемое, равное 2 2и так далее. Результат в любом случае будет представлять собой сумму степеней двойки.

Запишем первые 10 натуральных чисел в виде сумм степеней двойки, чтобы вы могли увидеть закономерность, которой они подчиняются.

Древние египтяне выполняли деление по схожему алгоритму, но в обратном порядке, то есть с помощью умножения. К примеру, при делении 92 на 9 они определяли число, на которое нужно умножить 9, чтобы получить 92. Сначала необходимо составить таблицу чисел. В левом столбце запишем последовательность степеней двойки, в правом столбце будем раз за разом удваивать 9, пока оно не превысит 92.

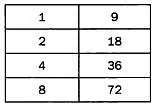
Теперь выберем из правого столбца числа, которые в сумме дают 92. Так как выбрать такие числа нельзя, 92 не делится на 9 нацело. Ближайшая сумма равна 18 + 72 = 90. Следовательно, результат деления равен 2 + 8 = 10 (сумме степеней двойки, соответствующих числам 18 и 72), остаток от деления равен 2.

Для счета необходимо дать величинам названия, а также предусмотреть символы для их обозначения. Сегодня символы, обозначающие цифры, являются практически универсальными и используются во всех уголках планеты. Названия чисел и слова, используемые при счете, также эквивалентны. Однако даже самый точный перевод не всегда может обеспечить соответствие исходных понятий.