Эдуардо Арройо - Том 42. Путешествие от частицы до Вселенной. Математика газовой динамики

На графике показано, что импульс частицы при любом ее положении один и тот же. Подобным образом движется, например, поезд, который всегда едет на одной и той же скорости.

Более интересен случай, когда частица движется зигзагом, например как игрушка, прикрепленная к пружине и подпрыгивающая вверх-вниз. В этом случае скорость игрушки уменьшается, пока она не доходит до одного края, затем она начинает увеличиваться по мере того, как игрушка доходит до центра движения, и затем снова уменьшается, когда она доходит до противоположного края. Форма такого движения в фазовом пространстве довольно любопытна.

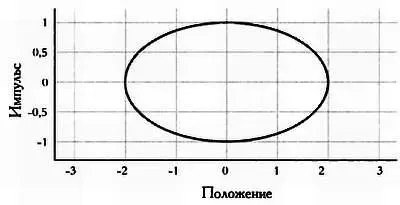
Как можно заметить, траектория имеет форму эллипса, то есть типичную форму колебательного движения, хотя возможны и более сложные случаи. Эта траектория соответствует некоторым начальным положению и скорости, то есть начальным условиям. С каждым набором начальных условий связана разная траектория в фазовом пространстве. На первом графике на стр. 46 показаны возможные траектории для частицы, движущейся зигзагом, в зависимости от ее начального положения.

* * *

РАЗЛИЧНЫЕ ТРАЕКТОРИИ В ФАЗОВОМ ПРОСТРАНСТВЕ

Существует огромное количество возможных траекторий в фазовом пространстве, и их форма зависит от правил, регулирующих развитие системы. Например, на графике показана траектория в фазовом пространстве частицы, которая колеблется под воздействием силы трения, так что постепенно теряет энергию.

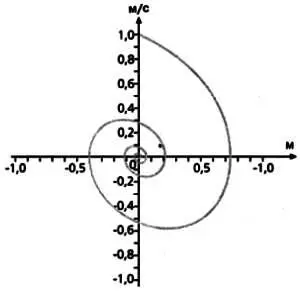
Но возможно и намного менее предсказуемое поведение. Рисунок ниже соответствует аттрактору Лоренца — траектории, возникающей при описании погоды. В целом существует столько возможных траекторий, сколько можно вообразить систем. Некоторые из них упорядочены, но существует и огромное количество систем, в которых траектория частицы непредсказуема. Трехмерная траектория абсолютно непредсказуема и никогда не проходит через одну и ту же точку.

* * *

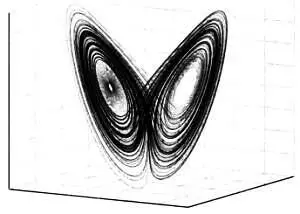
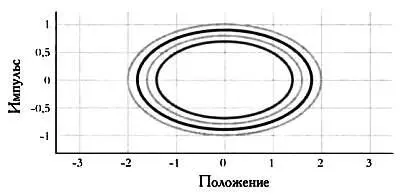
Различные траектории в фазовом пространстве.

Каждая траектория соответствует различной энергии.

В случае с газами мы хотим изучить не одну траекторию системы, а все возможные траектории; поскольку начальные условия нам неизвестны, следовательно, мы должны предположить, что они находятся в определенном диапазоне. Метод Гамильтона позволяет нам вывести некоторые свойства без необходимости останавливаться на каком-то из них конкретно. Одно из этих свойств, которое приобретет чрезвычайную важность при изучении газов, заключается в том, что траектории в фазовом пространстве никогда не пересекаются: невозможно прийти в одно и то же место, исходя из различных начальных условий, если только оба начальных условия не порождают один и тот же тип движения.

То есть представленное ниже невозможно.

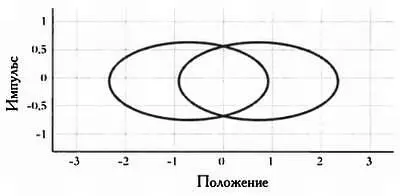
Кажется, что это противоречит здравому смыслу. Неужели действительно два объекта не могут пройти через одну и ту же точку? Не нужно забывать, что мы говорим о фазовом пространстве: в нем занять одну и ту же точку означает иметь одно и то же положение и один и тот же импульс, то есть одну и ту же скорость. Пред ставим себе, что в фазовом пространстве возможно пересечение траекторий, как на предыдущем графике. Это означало бы, что у частицы, которая находится в этой точке, есть выбор из двух возможных вариантов движения. Какой вариант она выберет? Возможно ли, чтобы законы физики приводили к разным результатам? Нет, это невозможно, и, следовательно, траектории не могут пересечься. Ни для одной из них невозможно разветвление.

Теперь у нас есть необходимые инструменты для изучения поведения газов. Мы знаем, что молекулы газа ведут себя в соответствии с принципом наименьшего действия, а также можем применить уравнения Гамильтона к произвольному числу частиц. Теперь нам осталось написать уравнения и начать их решать.

Конечно же, это титаническая работа. В литре газа приблизительно 10 23частиц, или двадцать три нуля после единицы. Поскольку для каждой частицы нужно шесть координат и для каждой координаты мы должны решить уравнение, перед нами — около квадриллиона уравнений. Даже если воспользоваться мощным компьютером, для решения этой задачи потребуются тысячи лет.