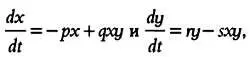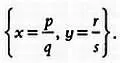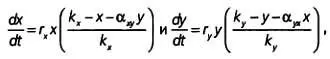Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

dy / dt = ry — sxy .

Одна из предпосылок моделей Вольтерры и Лотки заключалась в том, что отдельные особи, к примеру волки и зайцы, ведут себя подобно частицам газа. Проведя параллель с так называемым законом действующих масс, мы обнаружим, что число взаимодействий между хищниками и жертвами зависит от столь очевидных параметров, как число хищников х и число жертв у . По этой причине их взаимодействие обозначается произведением этих чисел, то есть х · у с соответствующими коэффициентами: qxy и — sxy .

Объединив два описанных выше дифференциальных уравнения в систему:

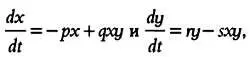
получим знаменитую систему уравнений Лотки — Вольтерры.

После того как мы учли взаимодействие хищников и жертв, решить эту систему уже не так просто, как раньше. В соответствии с моделью, при высокой численности жертв возрастет и число хищников, однако по мере поедания жертв популяция хищников также сократится. В свою очередь, ввиду снижения численности хищников число жертв вновь возрастет, и это вновь приведет к увеличению числа хищников.

Если представить подобные циклические колебания численности популяций на одном графике, мы получим цикл, имеющий название «цикл — решение», так как он является решением уравнений Лотки — Вольтерры.

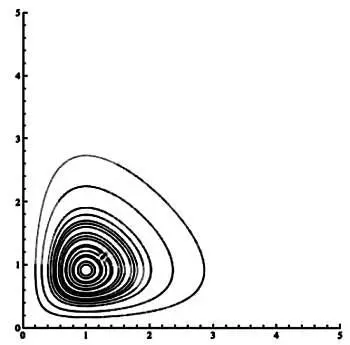
Модель «хищник — жертва» Лотки— Вольтерры: число хищников обозначено на оси у, число жертв — на оси х.

Получить «цикл — решение» системы уравнений можно разными способами, но самым важным из них является рассмотрение колебаний численности популяций. Форма цикла зависит от начального числа хищников и жертв.

Столь же нетрудно найти точку равновесия, так как ее координаты равны:

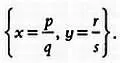
Нужно очень четко представлять себе описанные колебания системы, особенно когда речь идет о климатических моделях (о них мы поговорим в следующем разделе).

* * *

КОНКУРЕНЦИЯ МЕЖДУ ВИДАМИ

Помимо модели «хищник — жертва», Лотка и Вольтерра представили еще одну модель, описывающую конкуренцию между двумя популяциями или видами. Допустим, что две популяции конкурируют за один и тот же ресурс, при этом рост их численности описывается логистической моделью.

Обозначив через хи учисленность особей в популяциях, имеем:

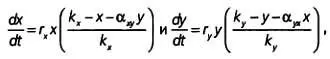
где r x, r у— коэффициенты роста, k x, k y— поддерживающие емкости для каждой популяции. Эти выражения также содержат коэффициенты α, описывающие взаимодействие между особями в популяциях. Иными словами, α xyобозначает воздействие, которое оказывает вид уна вид х, в то время как α yx- это воздействие хна у. Модель можно расширить для нескольких видов, однако это несколько усложнит анализ возможных ситуаций.

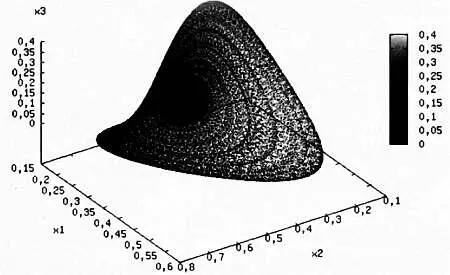
Модель межвидовой конкуренции Лотки— Вольтеррыдля четырех видов.

* * *

В последние десятилетия весьма актуальна тема глобального потепления. Хотя метеорологические центры составляют прогнозы погоды с применением сложных математических моделей, на их основании довольно трудно дать ответ на вопрос, действительно ли наблюдается глобальное изменение климата.

Математические модели, используемые в метеорологии, называются климатическими моделями. Они основаны на описаниях атмосферных процессов и компьютерном моделировании взаимодействия атмосферы и океанов, суши и шапок льда на полюсах. Эти модели представляют собой дифференциальные уравнения, в основе которых лежат законы физики. При их составлении поверхность Земли делится на квадраты, которые описываются уравнениями. Затем вычисляется скорость ветров, относительная влажность воздуха, теплопередача и так далее, а также взаимодействие между соседними областями. На основе интерпретации итоговых результатов моделирования метеорологи и составляют свои прогнозы.